Konverterer binær til decimal: Konverterer binær til decimal og omvendt.

---

Sådan konverteres Binære tal til Decimaltal:

• Trin 1: Skriv den vægt, der er knyttet til hvert ciffer i det binære tal, ned. Vægten er 2 gange potensen af cifferets position i tallet fra højre til venstre.
• Trin 2: Noter nu den vægt, for hvilken den binære værdi er lig med 1.
• Trin 3: Læg alle de tal sammen, der er opnået i det foregående trin
• Trin 4: Tallet fra det sidste trin er det decimale ækvivalent til det binære tal.

Lad os overveje en binær værdi 1101001.

1.) Første trin:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÆR} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Vægt i forbindelse med} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Andet trin: Vægte, for hvilke de binære cifre er 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Tredje trin: Tilføjelse af alle vægte

$$105 = 64 + 32 + 8 + 1$$

4.) Sidste trin: Det decimale udtryk for det binære er:: 105

Sådan konverteres Decimaltal til Binærtal:

Ved at følge disse trin kan du konvertere ethvert decimaltal til det binære system:

• Trin 1: Divider decimaltallet med 2 og skriv resten ned og tildel en værdi R1 = rest, og tildel værdien Q1 = kvotienten, der fremkommer ved denne division, på samme måde.
• Trin 2: Divider nu Q1 med 2 og noter resten. Tilknyt værdien af resten til R2 og værdien af kvotienten til Q1.
• Trin 3: Fortsæt sekvensen, indtil du på et tidspunkt i en division får værdien af kvotienten (Qn) lig med 0.
• Trin 4: Du kan skrive det binære tal som: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Eksempel: Lad os se på decimaltallet 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Nu kan du skrive det binære tal ned fra resten, begyndende med R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINÆR

Hvordan konverterer man cifre efter decimalkommaet mellem det binære og det decimale talsystem?

Indtil videre har vi lært, hvordan man konverterer hele tal mellem binære og decimale tal. Hvad med tal med decimaltal? Proceduren svarer til ovenstående trin. Først opdeles tallet i den del, der ligger før og efter decimaltallet. Lad os se på decimaltallet 1932.1875:

Den består af en heltalsdel 1932 og brøken 0,1875. For den hele taldel 1932 anvendes trinene fra ovenfor. Den resulterende binære ækvivalent er: 11110001100.

Brøkdelen 0,1875 kan omregnes efter følgende skema. Recursivt multiplicere den delvise del med to. Hvis resultatet er større end 1, skrives 1 ned, og der trækkes derefter 1 fra det resulterende tal. Hvis resultatet er mindre end 1, noteres 0. Fortsæt derefter med at gange med to. I modsat fald skrives 0 ned.

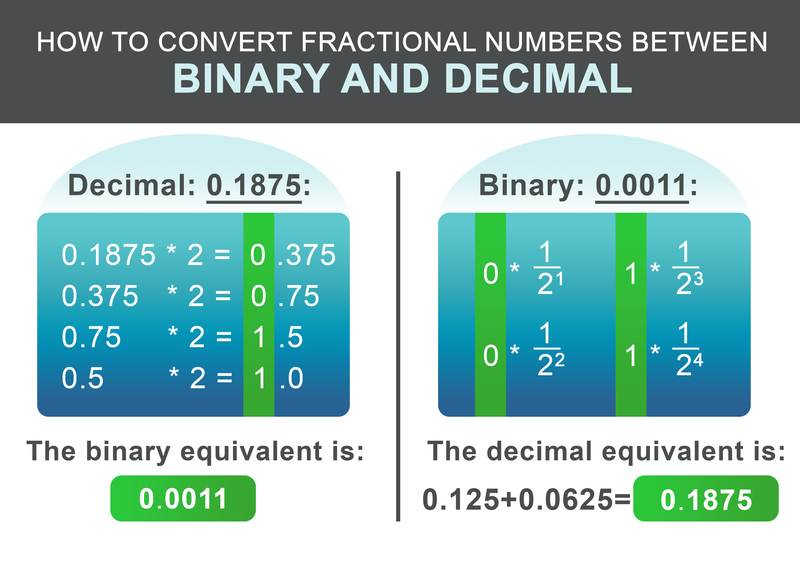
For vores eksempel 0,1875 er det resulterende binære tal: 0,0011 I det sidste trin lægges de hele og brøkdelene sammen:

$$11110001100.0011$$

For at konvertere den binære fraktion tilbage er arbejdsgangen endnu enklere. Tilføj $1/2^i$ for hvert ciffer efter punktet til resultatet, hvor i er placeringen af det efterfølgende ciffer fra venstre mod højre, startende ved 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Det binære talsystem og dets anvendelser

Et talsystem er et sæt af forskellige kombinationer af symboler, hvor hvert symbol har en bestemt vægt. De vigtigste kendetegn ved et talsystem er radix eller base, som definerer det samlede antal symboler, der anvendes i et bestemt talsystem. F.eks. er radix i det binære talsystem 2, og radix i det decimale talsystem er 10.

Det binære systems cifferrum

I det binære system har vi to forskellige cifre: I computere har vi enheder som f.eks. flip-flops, der kan lagre et af de to niveauer i henhold til et styresignal. Det højere niveau tildeles værdien 1, og det lavere niveau tildeles værdien 0, hvorved der dannes et binært system.

Betydningen af det binære system inden for databehandling:

En computer består af milliarder og atter milliarder af transistorer, der fungerer digitalt. Udtrykket digital vedrører de diskrete logiske niveauer. Logiske niveauer er de forskellige potentielle niveauer som f.eks. 5V, 0V, 10v og mange andre.

Enhver computer fungerer ved hjælp af binær logik, så hvis vi ønsker at repræsentere computeren, skal vi skrive tallene med radix lig med 2. De to symboler i dette talsystem svarer til de to diskrete logiske niveauer. For nemheds skyld betragter vi disse to symboler som 0 og 1, men for en computer er 0 og 1 forskellige spændingsniveauer. Generelt betragtes 0 som det lavere spændingsniveau og 1 som det højere spændingsniveau.

Alt, hvad vi ser på computerskærmen eller indtaster via musen eller tastaturet, er 0'er og 1'er, den eneste forskel er deres sekventielle placering. Så hvis vi ønsker at få vores arbejde udført af computeren, skal vi vide, hvordan binære funktioner fungerer, og hvad forholdet mellem binære og decimale tal er, så vi kan konvertere værdierne fra det binære område til vores kendte område.