Двоично-десятичный конвертер: конвертирует двоичную систему в десятичную и наоборот.

---

Как перевести двоичные числа в десятичные:

• Шаг 1: Запишите вес, связанный с каждой цифрой двоичного числа. Вес равен 2 по мощности позиции цифры в числе, читаемой справа налево.
• Шаг 2: Теперь запишите вес, для которого двоичное значение равно 1.
• Шаг 3: Сложите все числа, полученные на предыдущем этапе
• Шаг 4: Число, полученное на последнем шаге, будет десятичным эквивалентом двоичного числа.

Рассмотрим двоичное значение 1101001.

1.) Первый шаг:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Вес, связанный с} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Второй шаг: Веса, для которых двоичные цифры равны 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Третий шаг: Сложение всех весов

$$105 = 64 + 32 + 8 + 1$$

4.) Последний шаг: Десятичный эквивалент двоичного числа:: 105

Как перевести десятичные числа в двоичные:

Следуя этим шагам, вы можете перевести любое десятичное число в двоичную систему:

• Шаг 1: Разделите десятичное число на 2, запишите остаток и присвойте ему значение R1 = остаток, аналогично присвойте значение Q1 = полученный при делении коэффициент.
• Шаг 2: Теперь разделите Q1 на 2 и запишите остаток. Припишите значение остатка к R2, а значение делителя - к Q1.
• Шаг 3: Продолжайте последовательность до тех пор, пока в какой-то момент деления вы не получите значение коэффициента (Qn), равное 0.
• Шаг 4: Двоичное число можно записать в виде: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Пример: Рассмотрим десятичное число 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Теперь вы можете записать двоичное число из остатков, начиная с R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) ДЕЦИМАЛЬНЫЙ = (10110011) BINARY

Как преобразовать цифры после десятичной точки между двоичной и десятичной системой счисления?

До сих пор мы узнали, как преобразовывать целые числа в двоичные и десятичные. Как насчет чисел с десятичными знаками? Процедура похожа на описанные выше шаги. Сначала разделите число на часть до и после десятичного знака. Рассмотрим десятичное число 1932.1875:

Она состоит из целой части 1932 и дроби 0,1875. Для целой части 1932 используйте шаги, описанные выше. Полученный двоичный эквивалент имеет вид: 11110001100.

Дробная часть 0,1875 может быть преобразована по следующей схеме. Рекурсивно умножьте дробную часть на два. Если результат больше 1, запишите 1, а затем вычтите 1 из полученного числа. Если результат меньше единицы, запишите 0. Далее продолжите умножение на два. В противном случае запишите 0.

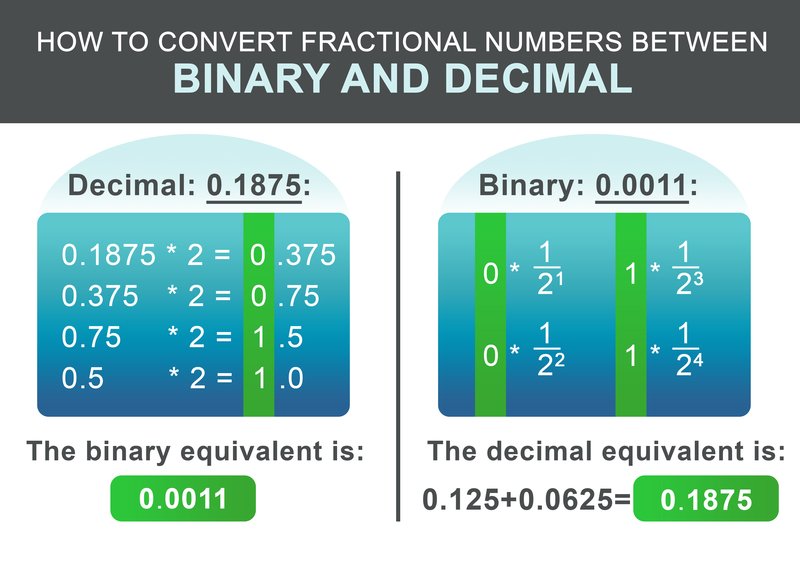
Для нашего примера 0.1875, полученное двоичное число будет: 0.0011 На последнем этапе сложите целую и дробную части:

$$11110001100.0011$$

Для обратного преобразования двоичной фракции рабочий процесс еще проще. Добавьте к результату $1/2^i$ для каждой цифры после точки, при этом i - это положение цифры после слева направо, начиная с 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Двоичная система счисления и ее применение

Система счисления - это набор различных комбинаций символов, каждый из которых имеет определенный вес. Основной характеристикой системы счисления является радикс или основание, определяющее общее количество символов, используемых в конкретной системе счисления. Например, радикс двоичной системы счисления равен 2, а радикс десятичной системы счисления равен 10.

Цифровое пространство двоичной системы

В двоичной системе у нас есть две отдельные цифры: 0 и 1. В компьютерах есть такие устройства, как флип-флопы, которые могут хранить любой из двух уровней в соответствии с управляющим сигналом. Старшему уровню присваивается значение 1, а младшему - 0, таким образом, формируется двоичная система.

Важность двоичной системы в вычислениях:

В компьютере используются миллиарды и миллиарды транзисторов, которые работают в цифровом режиме. Термин "цифровой" связан с дискретными логическими уровнями. Логические уровни - это различные потенциальные уровни, такие как 5 В, 0 В, 10 В и многие другие.

Любой компьютер работает с использованием двоичной логики, поэтому, если мы хотим представить компьютер, мы должны записывать числа с радиксом, равным 2. Два символа в этой системе счисления аналогичны двум дискретным логическим уровням. Для простоты мы считаем эти два символа 0 и 1, но для компьютера 0 и 1 - это разные уровни напряжения. Как правило, 0 считается младшим уровнем напряжения, а 1 - старшим.

Все, что мы видим на экране компьютера или вводим с помощью мыши или клавиатуры - это все 0 и 1, разница лишь в их последовательном расположении. Поэтому, если мы хотим выполнять свою работу на компьютере, мы должны знать, как работает двоичная система счисления и какова связь двоичной системы с десятичной, чтобы преобразовывать значения из двоичной области в известную нам область.