
Wie konvertiert man Binärzahlen in Dezimalzahlen:
- Schritt 1: Notieren Sie das Gewicht, das unter jeder Ziffer der Binärzahl steht. Das Gewicht ist 2 mal die Potenz der Position der Ziffer in der Zahl von rechts nach links gelesen.
- Schritt 2: Notieren Sie nun das Gewicht, für das der Binärwert gleich 1 ist.
- Schritt 3: Addiere alle im vorherigen Schritt erhaltenen Zahlen
- Schritt 4: Die Zahl aus dem letzten Schritt ist die dezimale Entsprechung der Binärzahl.
Betrachten wir einen binären Wert 1101001.
1.) Erster Schritt:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÄR} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Gewicht assoziiert} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Zweiter Schritt: Gewichte, bei denen die Binärziffern 1 sind.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Dritter Schritt: Addieren aller Gewichte
$$105 = 64 + 32 + 8 + 1$$
4.) Letzter Schritt: Das dezimale Äquivalent des Binärwertes ist:: 105
Wie man Dezimalzahlen in Binärzahlen umwandelt:
Mit diesen Schritten können Sie jede Dezimalzahl in das Binärsystem umwandeln:
- Schritt 1: Dividieren Sie die Dezimalzahl durch 2 und notieren Sie den Rest und weisen Sie den Wert R1 = Rest zu, ebenso den Wert Q1 = Quotient, den Sie bei dieser Division erhalten.
- Schritt 2: Dividiere nun Q1 durch 2 und notiere den Restbetrag. Weisen Sie den Wert des Restes R2 und den Wert des Quotienten Q1 zu.
- Schritt 3: Setzen Sie die Reihe fort, bis Sie irgendwann bei einer Division den Wert des Quotienten (Qn) gleich 0 erhalten.
- Schritt 4: Sie können die Binärzahl schreiben als: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINÄR
Wie konvertiert man Nachkommastellen zwischen dem binären und dem dezimalen Zahlensystem?
Bisher haben wir gelernt, wie man ganze Zahlen zwischen Binär- und Dezimalzahlen umwandelt. Wie sieht es mit Zahlen mit Nachkommastellen aus? Das Verfahren ist ähnlich wie die oben beschriebenen Schritte. Zunächst wird die Zahl in ihren Teil vor und nach der Dezimalstelle zerlegt. Betrachten wir die Dezimalzahl 1932,1875:
Sie besteht aus einem ganzzahligen Teil 1932 und dem Bruch 0,1875. Für den ganzzahligen Teil 1932 werden die oben beschriebenen Schritte durchgeführt. Die resultierende binäre Entsprechung ist: 11110001100.
Der Bruchteil 0,1875 kann nach folgendem Schema umgerechnet werden. Rekursiv multiplizieren Sie den Bruchteil mit zwei. Wenn das Ergebnis größer als 1 ist, schreibe 1 auf und ziehe dann 1 von der resultierenden Zahl ab. Wenn das Ergebnis kleiner als 1 ist, notiere 0. Fahre dann mit der Multiplikation mit zwei fort. Andernfalls notiere 0.
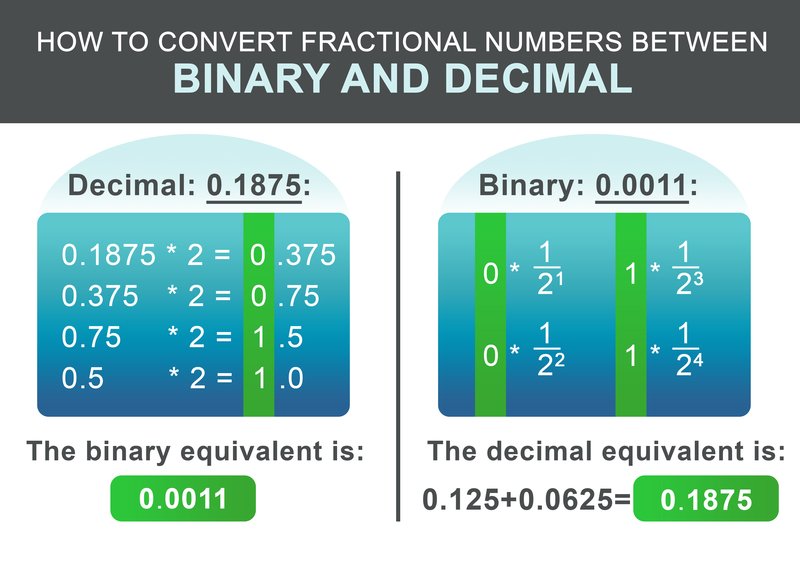
Für unser Beispiel 0,1875 lautet die resultierende Binärzahl: 0,0011 Im letzten Schritt werden die ganzzahligen und die gebrochenen Teile addiert:
$$11110001100.0011$$
Für die Rückkonvertierung der Binärfraktion ist der Arbeitsablauf noch einfacher. Addieren Sie $1/2^i$ für jede Ziffer nach dem Punkt zum Ergebnis, wobei i die Position der Nachkommastelle von links nach rechts ist, beginnend bei 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Das binäre Zahlensystem und seine Anwendungen
Ein Zahlensystem besteht aus einer Reihe verschiedener Kombinationen von Symbolen, wobei jedes Symbol ein bestimmtes Gewicht hat. Die wichtigsten Merkmale eines Zahlensystems sind die Radix oder Basis, die die Gesamtzahl der in einem bestimmten Zahlensystem verwendeten Symbole definiert. Die Basis des binären Zahlensystems ist zum Beispiel 2, die Basis des dezimalen Zahlensystems ist 10.
Der Ziffernraum des Binärsystems
Im Binärsystem haben wir zwei verschiedene Ziffern: 0 und 1. In Computern gibt es Geräte wie Flipflops, die eine der beiden Ebenen entsprechend einem Steuersignal speichern können. Der höheren Stufe wird der Wert 1 und der niedrigeren Stufe der Wert 0 zugewiesen, so dass ein binäres System entsteht.
Die Bedeutung des Binärsystems in der Informatik:
Ein Computer besteht aus Abermilliarden von Transistoren, die digital arbeiten. Der Begriff "digital" bezieht sich auf die diskreten Logikstufen. Logikpegel sind die verschiedenen Potenziale wie 5 V, 0 V, 10 V und viele andere.
Jeder Computer arbeitet mit einer binären Logik. Wenn wir also den Computer darstellen wollen, müssen wir die Zahlen mit der Radix 2 schreiben. Die beiden Symbole in diesem Zahlensystem entsprechen den beiden diskreten Logikstufen. Der Einfachheit halber betrachten wir diese beiden Symbole als 0 und 1, aber für einen Computer sind 0 und 1 unterschiedliche Spannungspegel. Im Allgemeinen wird 0 als der niedrigere Spannungspegel und 1 als der höhere Spannungspegel betrachtet.
Alles, was wir auf dem Bildschirm des Computers sehen oder über eine Maus oder eine Tastatur eingeben, sind 0en und 1en, der einzige Unterschied ist ihre sequentielle Anordnung. Wenn wir also unsere Arbeit mit dem Computer erledigen wollen, müssen wir wissen, wie das Binärsystem funktioniert und in welchem Verhältnis das Binärsystem zu den Dezimalzahlen steht, um die Werte aus dem Binärbereich in unseren bekannten Bereich zu konvertieren.
