Konverter for binært til titallsystem: Konverterer binært til titallsystem og vice versa.

---

Slik konverterer du binære tall til desimaltall:

• Trinn 1: Skriv ned vekten knyttet til hvert siffer i det binære tallet. Vekten er 2 opphøyd i posisjonen til sifferet i tallet, og leses fra høyre mot venstre.
• Trinn 2: Legg nå merke til den vekten som det binære tallet er lik 1.
• Trinn 3: Legg sammen alle tallene du fikk i forrige trinn
• Trinn 4: Tallet fra forrige trinn vil være den desimale ekvivalenten av det binære tallet.

La oss se på en binær verdi 1101001.

1. trinn:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÆR } & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Vekt er forbundet med } & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Andre trinn: Vekter der binære sifre er 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Tredje trinn: Legge til alle vektene

$$105 = 64 + 32 + 8 + 1$$

4.) Siste trinn: Den desimale ekvivalenten for binærkoden er: : 105

Slik konverterer du desimaltall til binærtall:

Ved å følge disse trinnene kan du konvertere ethvert desimalt tall til det binære systemet:

• Trinn 1: Del det desimale tallet med 2 og skriv opp resten og tildel en verdi R1 = rest, tilsvarende tildelingen av verdien Q1 = kvotient som er oppnådd i denne divisjonen.
• Trinn 2: Nå dividerer du Q1 med 2 og noterer resten. Tildel restverdien til R2 og kvotientverdien til Q1.
• Trinn 3: Fortsett sekvensen til du på et tidspunkt i en divisjon får kvotientens verdi (Qn) lik 0.
• Trinn 4: Det binære tallet kan skrives som: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Eksempel: La oss se på det desimale tallet 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Nå kan du skrive ned det binære tallet fra restene, og begynne med R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) TITALL = (10110011) BINÆR

Hvordan konverterer du sifre etter desimaltegnet mellom det binære og det desimale tallsystemet?

Hittil har vi lært hvordan vi konverterer heltall mellom binært og desimalt. Hva med tall med desimaler? Prosedyren er lik prosedyren over. Først deles tallet i den delen som er før og etter desimaltegnet. La oss se på det desimale tallet 1932,1875:

Den består av en heltallsdel 1932 og brøken 0,1875. For heltallsdelen 1932, bruk trinnene ovenfor. Det resulterende binære tallet er: 11110001100.

Den brøkete delen 0,1875 kan konverteres i henhold til følgende skjema. Multipliser den brøkete delen med to ved resirkulering. Hvis resultatet er større enn 1, skriv ned 1 og trekk deretter 1 fra det resulterende tallet. Hvis resultatet er mindre enn én, skriv ned 0. Fortsett deretter å multiplisere med to. Ellers, skriv ned 0.

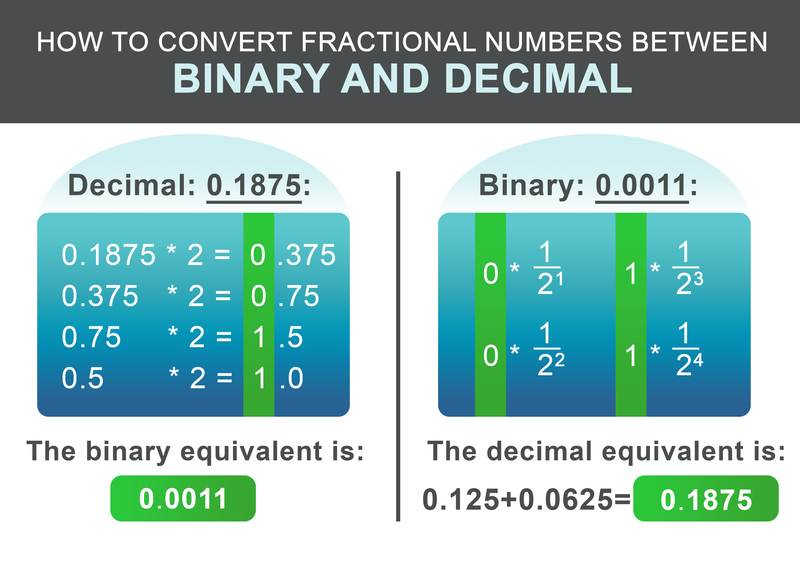
For vårt eksempel 0.1875 blir det resulterende binære nummeret: 0.0011 I det siste trinnet legger du sammen heltalls- og brøkdelen:

$$11110001100.0011$$

For å konvertere det binære brøket tilbake, er arbeidsflyten enda enklere. Legg til $1/2^i$ for hver siffer etter punktumet i resultatet, der i er posisjonen til sifferet fra venstre mot høyre, med start i 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Det binære tallsystemet og dets bruksområder

Et tallsystem er en mengde ulike kombinasjoner av symboler, der hvert symbol har en bestemt vekt. De viktigste kjennetegnene ved et tallsystem er radikset eller basen, som definerer det totale antallet symboler som brukes i et bestemt tallsystem. Radikset i det binære tallsystemet er for eksempel 2, og radikset i det desimale tallsystemet er 10.

Tallrommet til det binære systemet

I det binære systemet har vi to forskjellige siffer: 0 og 1. I datamaskiner har vi enheter som flip-floper som kan lagre hvilket som helst av de to nivåene i henhold til et kontrollsignal. Det høyere nivået tildeles verdien 1 og det lavere nivået tildeles verdien 0, og danner dermed et binært system.

Betydningen av det binære systemet i databehandling:

En datamaskin benytter seg av milliarder og atter milliarder transistorer som opererer digitalt. Begrepet digitalt har å gjøre med de diskrete logikknivåene. Logikknivåer er de ulike potensialnivåene som 5V, 0V, 10V og mange andre.

Enhver datamaskin bruker en binær logikk, så hvis vi vil representere datamaskinen, må vi skrive tallene med grunntall lik 2. De to symbolene i dette tallsystemet er analoge med de to diskrete logikknivåene. For vår egen del betrakter vi disse to symbolene som 0 og 1, men for en datamaskin er 0 og 1 ulike spenningsnivåer. Generelt sett regnes 0 for det laveste spenningsnivået, og 1 regnes for det høyeste spenningsnivået.

Alt vi ser på dataskjermen eller gir som inndata via en mus eller tastatur er nuller og énere, den eneste forskjellen er deres sekvensielle ordning. Så, hvis vi vil ha datamaskinen til å gjøre arbeidet vårt for oss, må vi vite hvordan binærtall fungerer, og hvilket forhold binærtall har til titallsystemet for å konvertere verdier fra det binære domenet til vårt kjente domene.