Konverterare från binär till decimal: Konverterar binär till decimal och vice versa.

---

Hur man konverterar binära tal till decimal:

• Steg 1: Skriv ner vikten under varje siffra i det binära talet. Vikten är 2 gånger potensen av siffrans position i talet från höger till vänster.
• Steg 2: Notera nu den vikt för vilken det binära värdet är lika med 1.
• Steg 3: Addera alla de tal som du fick i föregående steg.
• Steg 4: Siffran från det sista steget är den decimala motsvarigheten till det binära talet.

Låt oss betrakta ett binärt värde 1101001.

1.) Första steget:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÄR} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Vikt i samband med detta} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Andra steget: Vikter för vilka de binära siffrorna är 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Tredje steget: Lägg ihop alla vikter.

$$105 = 64 + 32 + 8 + 1$$

4.) Sista steget: Den decimala motsvarigheten till det binära är:: 105

Hur man konverterar decimaltal till binärt tal:

Genom att följa dessa steg kan du konvertera alla decimaltal till binärt system:

• Steg 1: Dividera decimaltalet med 2 och skriv ner återstoden och tilldela ett värde R1 = återstoden, och tilldela på samma sätt värdet Q1 = den kvot som erhålls vid denna division.
• Steg 2: Dela nu Q1 med 2 och notera återstoden. Tilldela värdet av återstoden till R2 och värdet av kvoten till Q1.
• Steg 3: Fortsätt sekvensen tills du någon gång i en division får ett kvotvärde (Qn) som är lika med 0.
• Steg 4: Du kan skriva det binära talet som: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Exempel: Låt oss betrakta decimaltalet 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Nu kan du skriva ner det binära talet från resttalen, med början med R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINÄR

Hur konverterar man siffror efter decimalpunkten mellan det binära och decimala talsystemet?

Hittills har vi lärt oss hur man omvandlar heltalstal mellan binära och decimala tal. Hur är det med tal med decimaler? Proceduren liknar stegen ovan. Dela först upp talet i dess del före och efter decimalplatsen. Låt oss betrakta decimaltalet 1932,1875:

Den består av en heltalsdel 1932 och bråkdelen 0,1875. För den heltaliga delen 1932 använder du stegen ovan. Den resulterande binära motsvarigheten är: 11110001100.

Bråkdelen 0,1875 kan konverteras enligt följande schema. Multiplicera den fraktionella delen rekursivt med två. Om resultatet är större än 1, skriv ner 1 och subtrahera sedan 1 från det resulterande talet. Om resultatet är mindre än ett skriver du ner 0. Fortsätt sedan att multiplicera med två. Om inte, skriv ner 0.

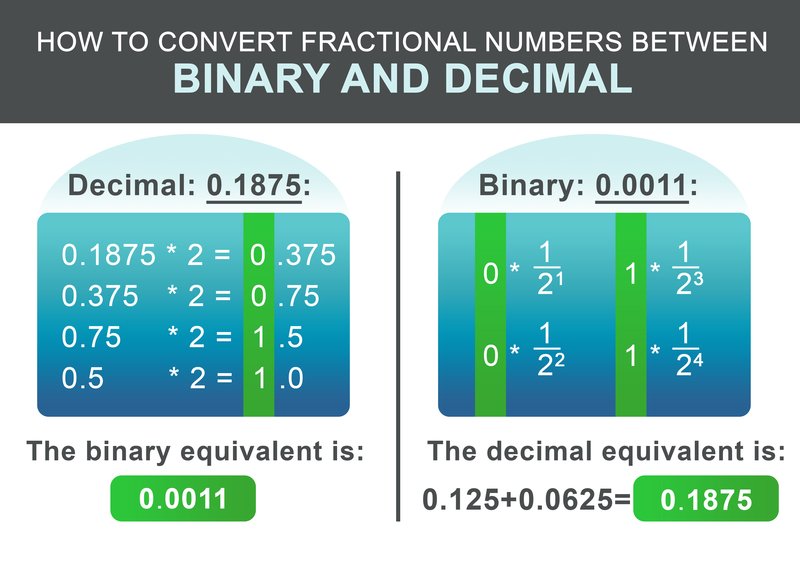
För vårt exempel 0,1875 blir det binära talet: 0,0011 I det sista steget adderas heltals- och bråkdelarna:

$$11110001100.0011$$

För att konvertera den binära fraktionen tillbaka är arbetsflödet ännu enklare. Lägg till $1/2^i$ för varje siffra efter pricken till resultatet, där i är siffrans position efter från vänster till höger, med början vid 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Det binära talsystemet och dess tillämpningar

Ett talsystem är en uppsättning olika kombinationer av symboler, där varje symbol har en specifik vikt. De viktigaste egenskaperna hos ett talsystem är radix eller bas som definierar det totala antalet symboler som används i ett visst talsystem. Till exempel är radix för det binära talsystemet 2 och radix för det decimala talsystemet 10.

Det binära systemets sifferutrymme

I det binära systemet har vi två olika siffror: I datorer har vi anordningar som flip-flops som kan lagra någon av de två nivåerna enligt en styrsignal. Den högre nivån tilldelas värdet 1 och den lägre nivån tilldelas värdet 0, vilket bildar ett binärt system.

Betydelsen av det binära systemet inom databehandling:

En dator består av miljarder och åter miljarder transistorer som arbetar digitalt. Termen digital avser de diskreta logiska nivåerna. Logiska nivåer är de olika potentiella nivåerna som 5V, 0V, 10V och många andra.

Alla datorer arbetar med binär logik, så om vi vill representera datorn måste vi skriva siffrorna med radix 2. De två symbolerna i detta talsystem motsvarar de två diskreta logiska nivåerna. För att underlätta för oss betraktar vi dessa två symboler som 0 och 1, men för en dator är 0 och 1 olika spänningsnivåer. I allmänhet anses 0 vara den lägre spänningsnivån och 1 den högre spänningsnivån.

Allt vi ser på datorskärmen eller ger inmatning via musen eller tangentbordet är 0:or och 1:or, den enda skillnaden är att de är ordnade i sekvens. Så om vi vill få vårt arbete utfört från datorn måste vi veta hur binärsystemet fungerar och hur binärsystemet förhåller sig till decimalerna för att omvandla värdena från den binära domänen till vår kända domän.