
2進数から10進数への変換方法。
- ステップ1: 2進数の各桁の下に関連する重みを書き留める。重みは、右から左へ読む数字の桁の位置の2乗とする。
- ステップ2:ここで、バイナリ値が1に等しい重みに注目する。
- ステップ3:前のステップで得られたすべての数値を加算する
- ステップ4:最後のステップの数値は、2進数の10進数に相当する数値になります。
2進数の値1101001を考えてみよう。
1.)最初のステップ
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{バイナリ} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{重量関連} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.)第2段階 2進数が1である重み
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.)第3段階すべての重みを足し合わせる
$$105 = 64 + 32 + 8 + 1$$
4.)最後のステップです。バイナリに相当する10進数は次のとおりです。: 105
10進数から2進数への変換方法。
以下の手順で、任意の10進数を2進数に変換することができます。
- 手順1:10進数を2で割って余りを書き出し、値R1=余りを割り当て、同様に値Q1=この割り算で得られた商を割り当てる。
- 手順2:Q1 を 2 で割って余りを求めます。余りの値を R2 に、商の値を Q1 に代入する。
- ステップ3: 割り算のある時点で商(Qn)の値が0になるまで、このシーケンスを続けます。
- ステップ4:2進数は次のように書けます。 $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) デシマル = (10110011) バイナリ
2進法と10進法の間で、小数点以下の数字をどのように変換するのですか?
これまで、整数を2進数と10進数の間で変換する方法を学びました。では、10進数のある数値はどうでしょうか。手順は、上記の手順と同様です。まず、数字を小数点の前後の部分に分割します。10進数の1932.1875を考えてみましょう。
整数部1932と分数0.1875からなる。整数部1932には、上記の手順を使用する。その結果、2進数の等価値は11110001100.
分数部0.1875は,以下のスキーマに従って変換することができる。分数部を再帰的に2倍する。 結果が1を超えたら、1を書き、結果の数から1を引く。結果が1より小さければ0を書き込む。次に2倍を続ける。 そうでなければ、0を書き留める。
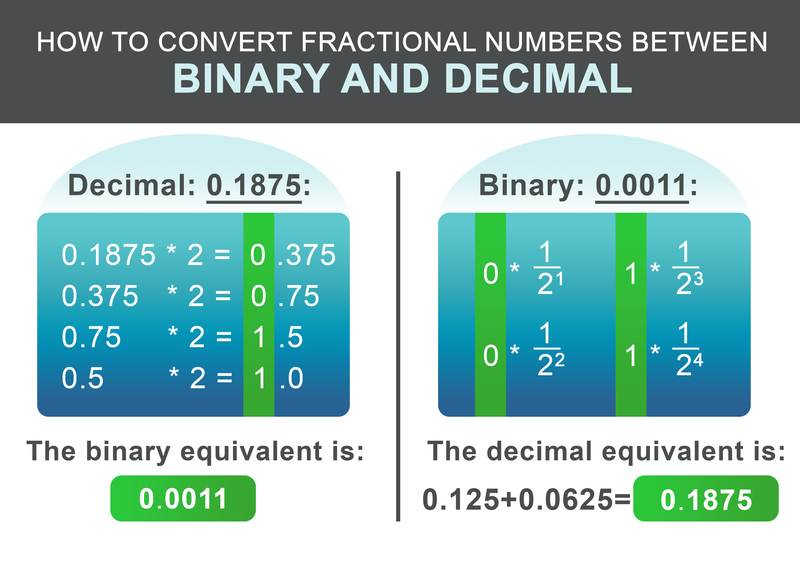
0.1875の例では、結果の2進数は0.0011となります。
$$11110001100.0011$$
2進数の派閥を逆変換する場合、ワークフローはさらに単純になる。 ドットの後の各桁について$1/2^i$を結果に加える。ここで、iは左から右へ、1から始まる後の桁の位置である。
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
二進法とその応用
数体系とは、記号の異なる組み合わせの集合であり、各記号には特定の重みがある。数システムの主な特徴は、特定の数システムで使用される記号の総数を定義する基数または基数です。例えば、2進数の基数は2であり、10進数の基数は10である。
2進法の桁空間
2進法では、0と1の2つの数字があります。コンピュータにはフリップフロップのようなデバイスがあり、制御信号に従って2つのレベルのいずれかを記憶することができる。上位のレベルには値1が、下位のレベルには値0が割り当てられており、2進法が成立している。
計算機における2進法の重要性。
コンピュータは、何十億というトランジスタを利用して、デジタル的に動作している。デジタルという言葉は、離散的な論理レベルに関するものである。論理レベルとは、5V、0V、10Vなど、さまざまな電位レベルのことである。
どんなコンピュータも2進数の論理で動作しているので、コンピュータを表現する場合、基数が2に等しい数字を書かなければならない。この数体系における2つの記号は、2つの離散論理レベルと類似している。ここでは便宜上、この2つの記号を0と1として考えるが、コンピュータにとって0と1は異なる電圧レベルである。一般に、0は低い方の電圧レベル、1は高い方の電圧レベルとみなされる。
私たちがコンピュータの画面上で見るもの、あるいはマウスやキーボードから入力するものは、すべて0と1であり、違いはその連続的な配列だけです。ですから、コンピュータで仕事をする場合、2進数の仕組みと、2進数と小数の関係を知って、2進数の領域から既知の領域に値を変換する必要があります。
