
Hoe zet je binaire getallen om in decimale:
- Stap 1: Noteer het gewicht onder elk cijfer van het binaire getal. Het gewicht is 2 tot de macht van de positie van het cijfer in het getal, van rechts naar links.
- Stap 2: Noteer nu het gewicht waarvoor de binaire waarde gelijk is aan 1.
- Stap 3: Tel alle getallen op die in de vorige stap zijn verkregen
- Stap 4: Het getal uit de laatste stap is het decimale equivalent van het binaire getal.
Laten we een binaire waarde 1101001 beschouwen.
1.) Eerste stap:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Gewicht geassocieerd} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Tweede stap: Gewichten waarvoor binaire cijfers 1 zijn.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Derde stap: Het optellen van alle gewichten
$$105 = 64 + 32 + 8 + 1$$
4.) Laatste stap: Het Decimale equivalent van het Binaire is:: 105
Hoe decimale getallen omzetten naar binaire:
Met deze stappen kunt u elk decimaal getal omzetten in het binaire stelsel:
- Stap 1: Deel het decimale getal door 2 en schrijf de rest op en ken een waarde R1 = rest toe, op dezelfde wijze de waarde Q1 = quotiënt verkregen bij deze deling.
- Stap 2: Deel nu Q1 door 2 en noteer de rest. Wijs de waarde van de rest toe aan R2 en de waarde van het quotiënt aan Q1.
- Stap 3: Ga door met de reeks totdat op een bepaald punt in een deling de waarde van het quotiënt (Qn) gelijk is aan 0.
- Stap 4: Je kunt het binaire getal schrijven als: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMALE = (10110011) BINARY
Hoe zet je cijfers achter de komma om tussen het binaire en het decimale getallenstelsel?
Tot nu toe hebben we geleerd hoe we gehele getallen kunnen omrekenen tussen binair en decimaal. Hoe zit het met getallen met decimale plaatsen? De procedure is vergelijkbaar met de stappen hierboven. Splits eerst het getal in zijn deel voor en na de decimaal. Laten we eens kijken naar het decimale getal 1932.1875:
Het bestaat uit een geheel deel 1932 en de breuk 0,1875. Voor het gehele getal 1932 gebruikt u de stappen van hierboven. Het resulterende binaire equivalent is: 11110001100.
Het breukdeel 0,1875 kan worden omgezet volgens het volgende schema. Vermenigvuldig het breukdeel recursief met twee. Als het resultaat groter is dan 1, schrijf dan 1 op en trek vervolgens 1 af van het resulterende getal. Als het resultaat kleiner is dan 1, schrijf dan 0. Ga dan verder met vermenigvuldigen met twee. Anders schrijf je 0 op.
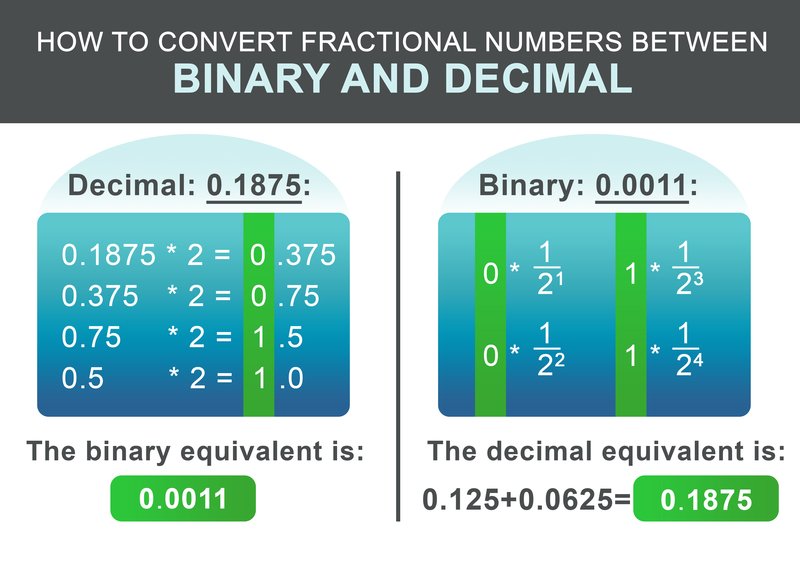
Voor ons voorbeeld 0,1875, is het resulterende binaire getal: 0,0011 In de laatste stap worden het gehele getal en de breuk opgeteld:
$$11110001100.0011$$
Voor het omzetten van het binaire factie terug is de workflow nog eenvoudiger. Voeg $1/2^i$ voor elk cijfer na de punt toe aan het resultaat, waarbij i de positie is van het cijfer na van links naar rechts, beginnend bij 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Het binaire getallenstelsel en zijn toepassingen
Een getallenstelsel is een verzameling van verschillende combinaties van symbolen, waarbij elk symbool een specifiek gewicht heeft. De belangrijkste kenmerken van een getallenstelsel zijn de radix of basis die het totale aantal symbolen bepaalt dat in een bepaald getallenstelsel wordt gebruikt. De radix van het binaire getallenstelsel is bijvoorbeeld 2, en de radix van het decimale getallenstelsel is 10.
De cijferruimte van het binaire stelsel
In het binaire systeem hebben we twee verschillende cijfers: 0 en 1. In computers hebben we apparaten zoals flip-flops die elk van de twee niveaus kunnen opslaan volgens een controlesignaal. Aan het hogere niveau wordt de waarde 1 toegekend en aan het lagere niveau de waarde 0, waardoor een binair systeem ontstaat.
Het belang van het binaire systeem in de informatica:
Een computer maakt gebruik van miljarden en miljarden transistors die digitaal werken. De term digitaal heeft betrekking op de discrete logische niveaus. Logische niveaus zijn de verschillende potentiaalniveaus zoals 5V, 0V, 10V, en vele andere.
Elke computer werkt met een binaire logica, dus als we de computer willen voorstellen, moeten we de getallen schrijven met een radix gelijk aan 2. De twee symbolen in dit getallensysteem zijn analoog aan de twee discrete logische niveaus. Voor ons gemak beschouwen wij deze twee symbolen als 0 en 1, maar voor een computer zijn 0 en 1 verschillende spanningsniveaus. In het algemeen wordt 0 beschouwd als het laagste spanningsniveau en 1 als het hoogste spanningsniveau.
Alles wat we op het scherm van de computer zien of invoeren via een muis of toetsenbord zijn allemaal 0's en 1's, het enige verschil is hun opeenvolgende rangschikking. Als wij dus ons werk met de computer willen doen, moeten wij weten hoe binair werkt en wat de relatie is van binair met decimalen om de waarden van het binaire domein om te zetten in ons bekende domein.
