
Cum se convertesc numerele binare în numere zecimale:
- Pasul 1: Scrieți greutatea asociată sub fiecare cifră a numărului binar. Ponderea este egală cu 2 la puterea puterii poziției cifrei în număr, citind de la dreapta la stânga.
- Pasul 2: Acum notați ponderea pentru care valoarea binară este egală cu 1.
- Pasul 3: Adunați toate numerele obținute în pasul anterior.
- Pasul 4: Numărul de la ultimul pas va fi echivalentul zecimal al numărului binar.
Să luăm în considerare o valoare binară 1101001.
1.) Primul pas:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARIE} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Greutate asociată} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) A doua etapă: Ponderi pentru care cifrele binare sunt 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Al treilea pas: Adăugarea tuturor ponderilor
$$105 = 64 + 32 + 8 + 1$$
4.) Ultima etapă: Echivalentul zecimal al binarului este:: 105
Cum se convertesc numerele zecimale în numere binare:
Urmând acești pași, puteți converti orice număr zecimal în sistemul binar:
- Pasul 1: Se împarte numărul zecimal la 2 și se notează restul și se atribuie o valoare R1 = restul, în mod similar se atribuie valoarea Q1 = coeficientul obținut la această împărțire.
- Pasul 2: Acum împărțiți Q1 cu 2 și notați restul. Atribuiți valoarea restului la R2 și valoarea cuplului la Q1.
- Pasul 3: Continuați secvența până când, la un moment dat, într-o împărțire, veți obține valoarea cutiorului (Qn) egală cu 0.
- Pasul 4: Puteți scrie numărul binar ca: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARIE
Cum se face conversia cifrelor după virgulă între sistemul binar și cel zecimal?
Până acum, am învățat cum să convertim numere întregi între binar și zecimal. Dar cum rămâne cu numerele cu zecimale? Procedura este similară cu pașii de mai sus. În primul rând, împărțiți numărul în partea sa de dinainte și de după zecimală. Să luăm în considerare numărul zecimal 1932,1875:
Acesta este format dintr-o parte întreagă 1932 și fracția 0,1875. Pentru partea întreagă 1932, utilizați pașii de mai sus. Echivalentul binar rezultat este: 11110001100.
Partea fracționară 0,1875 poate fi convertită în conformitate cu următoarea schemă. Se înmulțește recursiv partea fracționară cu doi. Dacă rezultatul depășește 1, scrieți 1 și apoi scădeți 1 din numărul rezultat. Dacă rezultatul este mai mic de 1, scrieți 0. În continuare, continuați să înmulțițiți cu doi. În caz contrar, scrieți 0.
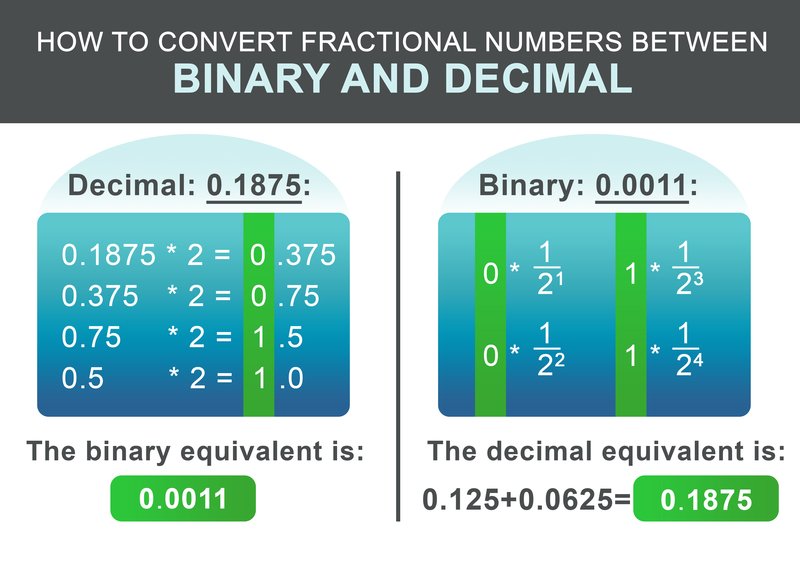
Pentru exemplul nostru 0,1875, numărul binar rezultat este: 0,0011 În ultimul pas se adaugă părțile întregi și fracționare:
$$11110001100.0011$$
Pentru a converti fracțiunea binară înapoi, fluxul de lucru este chiar mai simplu. Adăugați la rezultat $1/2^i$ pentru fiecare cifră de după punct, unde i este poziția cifrei de după, de la stânga la dreapta, începând de la 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Sistemul numeric binar și aplicațiile sale
Un sistem numeric este un set de combinații diferite de simboluri, fiecare simbol având o pondere specifică. Principalele caracteristici ale unui sistem de numere sunt radixul sau baza care definește numărul total de simboluri utilizate într-un anumit sistem de numere. De exemplu, radixul sistemului binar de numerație este 2, iar radixul sistemului zecimal de numerație este 10.
Spațiul de cifre al sistemului binar
În sistemul binar, avem două cifre distincte: 0 și 1. În calculatoare, avem dispozitive precum flip-flops care pot stoca oricare dintre cele două niveluri în funcție de un semnal de control. Nivelului superior i se atribuie valoarea 1, iar nivelului inferior i se atribuie valoarea 0, formând astfel un sistem binar.
Importanța sistemului binar în informatică:
Un computer utilizează miliarde și miliarde de tranzistori care funcționează în mod digital. Termenul digital se referă la nivelurile logice discrete. Nivelurile logice sunt diferitele niveluri de potențial, cum ar fi 5V, 0V, 10v și multe altele.
Orice calculator funcționează folosind o logică binară, astfel încât, dacă dorim să reprezentăm calculatorul, trebuie să scriem numerele cu radixul egal cu 2. Cele două simboluri din acest sistem de numerație sunt analoage celor două niveluri logice discrete. Pentru ușurința noastră, considerăm aceste două simboluri ca fiind 0 și 1, dar pentru un calculator 0 și 1 sunt niveluri de tensiune diferite. În general, 0 este considerat pentru nivelul de tensiune inferior, iar 1 este considerat pentru nivelul de tensiune superior.
Tot ceea ce vedem pe ecranul computerului sau tot ceea ce introducem prin intermediul mouse-ului sau al tastaturii sunt toți 0 și 1, singura diferență fiind aranjamentul lor secvențial. Așadar, dacă vrem să ne facem treaba cu ajutorul calculatorului, trebuie să știm cum funcționează binarul și care este relația dintre binar și zecimale pentru a converti valorile din domeniul binar în domeniul nostru cunoscut.
