Konverter Biner ke Desimal: Mengubah biner ke desimal dan sebaliknya.

---

Bagaimana cara mengubah Bilangan Biner ke Desimal:

• Langkah 1: Tuliskan bobot yang terkait di bawah setiap digit dari bilangan biner. Bobotnya adalah 2 pangkat dari posisi digit dalam angka yang dibaca dari kanan ke kiri.
• Langkah 2: Sekarang perhatikan bobot yang nilai binernya sama dengan 1.
• Langkah 3: Tambahkan semua angka yang diperoleh pada langkah sebelumnya
• Langkah 4: Angka dari langkah terakhir akan menjadi ekuivalen desimal dari bilangan biner.

Mari kita pertimbangkan nilai biner 1101001.

1.) Langkah pertama:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Berat badan yang terkait} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Langkah kedua: Bobot yang digit binernya adalah 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Langkah ketiga: Menambahkan semua bobot

$$105 = 64 + 32 + 8 + 1$$

4.) Langkah terakhir: Ekuivalen Desimal dari Biner adalah:: 105

Bagaimana cara mengubah Bilangan Desimal ke Biner:

Dengan mengikuti langkah-langkah ini, Anda dapat mengonversi angka desimal apa pun ke dalam sistem biner:

• Langkah 1: Bagilah bilangan desimal dengan 2 dan tuliskan sisanya dan tetapkan nilai R1 = sisa, dengan cara yang sama menetapkan nilai Q1 = hasil bagi yang diperoleh dalam pembagian ini.
• Langkah 2: Sekarang bagi Q1 dengan 2 dan catat sisanya. Tetapkan nilai sisa ke R2 dan nilai hasil bagi ke Q1.
• Langkah 3: Lanjutkan urutannya sampai pada suatu titik dalam pembagian Anda mendapatkan nilai hasil bagi (Qn) sama dengan 0.
• Langkah 4: Anda bisa menulis bilangan biner sebagai: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Contoh: Mari kita perhatikan bilangan desimal 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Sekarang Anda bisa menuliskan bilangan biner dari sisa-sisa, dimulai dengan R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINARY

Bagaimana Anda mengonversi digit setelah titik desimal antara sistem angka biner dan desimal?

Sejauh ini, kita telah belajar bagaimana mengkonversi bilangan bulat antara biner dan desimal. Bagaimana dengan bilangan dengan tempat desimal? Prosedurnya mirip dengan langkah-langkah di atas. Pertama, pisahkan angka menjadi bagian sebelum dan sesudah tempat desimal. Mari kita pertimbangkan angka desimal 1932.1875:

Ini terdiri dari bagian bilangan bulat 1932 dan pecahan 0.1875. Untuk bagian bilangan bulat 1932, gunakan langkah-langkah dari atas. Ekuivalen biner yang dihasilkan adalah: 11110001100.

Bagian pecahan 0.1875 bisa dikonversikan menurut skema berikut ini. Secara rekursif kalikan bagian pecahan dengan dua. Jika hasilnya melebihi 1, tuliskan 1 dan kemudian kurangi 1 dari angka yang dihasilkan. Jika hasilnya kurang dari satu, tuliskan 0. Selanjutnya, lanjutkan mengalikan dengan dua. Jika tidak, tuliskan 0.

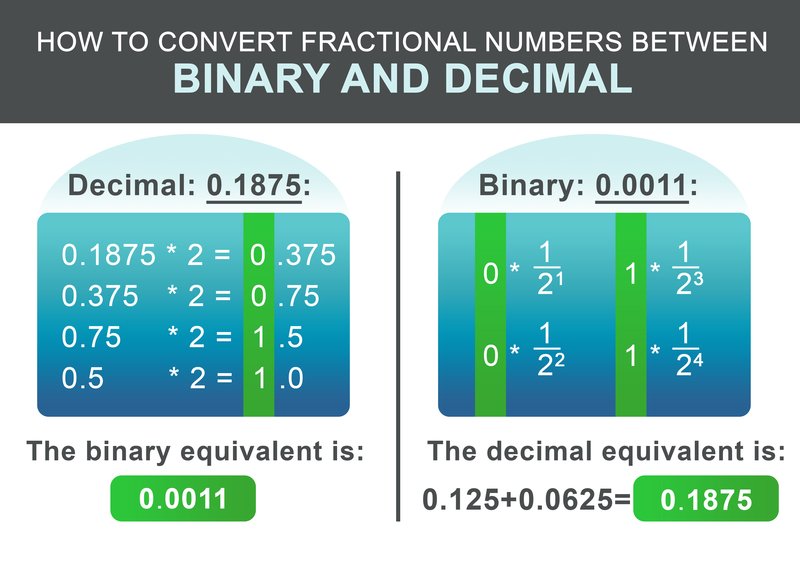
Untuk contoh kita 0.1875, bilangan biner yang dihasilkan adalah: 0.0011 Pada langkah terakhir tambahkan bagian bilangan bulat dan pecahan:

$$11110001100.0011$$

Untuk mengkonversi kembali faksi biner, alur kerjanya bahkan lebih sederhana. Tambahkan $1/2^i$ untuk setiap digit setelah titik ke hasilnya, dimana i adalah posisi digit setelahnya dari kiri ke kanan, dimulai dari 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Sistem Bilangan Biner dan Aplikasinya

Sistem bilangan adalah sekumpulan kombinasi simbol yang berbeda, dengan setiap simbol memiliki bobot tertentu. Karakteristik utama dari sistem bilangan adalah radix atau basis yang mendefinisikan jumlah total simbol yang digunakan dalam sistem bilangan tertentu. Misalnya, radix dari sistem bilangan biner adalah 2, dan radix dari sistem bilangan desimal adalah 10.

Ruang Digit dari Sistem Biner

Dalam sistem biner, kita memiliki dua digit yang berbeda: 0 dan 1. Dalam komputer, kita memiliki perangkat seperti flip-flop yang dapat menyimpan salah satu dari dua level menurut sinyal kontrol. Level yang lebih tinggi diberi nilai 1 dan level yang lebih rendah diberi nilai 0, sehingga membentuk sistem biner.

Pentingnya Sistem Biner dalam Komputasi:

Komputer memanfaatkan miliaran transistor yang beroperasi secara digital. Istilah digital berkaitan dengan level logika diskrit. Level logika adalah level potensial yang berbeda seperti 5V, 0V, 10v, dan banyak lainnya.

Setiap komputer beroperasi menggunakan logika biner, jadi jika kita ingin merepresentasikan komputer, kita harus menulis angka dengan radix sama dengan 2. Dua simbol dalam sistem bilangan ini analog dengan dua level logika diskrit. Untuk memudahkan kita, kita menganggap kedua simbol ini sebagai 0 dan 1, tetapi untuk komputer 0 dan 1 adalah level tegangan yang berbeda. Umumnya, 0 dianggap untuk level tegangan yang lebih rendah dan 1 dianggap untuk level tegangan yang lebih tinggi.

Semua yang kita lihat di layar komputer atau memberikan input melalui mouse atau keyboard semuanya adalah 0 dan 1, satu-satunya perbedaan adalah susunan urutannya. Jadi, jika kita ingin menyelesaikan pekerjaan kita dari komputer, kita harus tahu bagaimana biner bekerja dan apa hubungan biner dengan desimal untuk mengubah nilai dari domain biner menjadi domain yang kita ketahui.