
如何將二進位數轉換為十進位:
- 第一步:在二進制數字的每個位數下方寫下對應的權重。權重是2的該數字位數位置的次方。
- 步驟2:現在請注意當二進位值等於1時的重量。
- 在第三步骤中,将在前一步骤中获得的所有数字相加。
- 步驟4: 上一步得到的數字將是二進位數的十進制等價值。
1101001 的二進位值是什麼?
1.) 第一步:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{二進制} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{與重量相關} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) 第二步: 二進位數字為1的權重。
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) 第三步:將所有的重量相加
$$105 = 64 + 32 + 8 + 1$$
4.) 最後一步:二進位的十進制等於:: 105
如何將十進制數字轉換為二進制:
以下是将任意十进制数转换为二进制系统的步骤: 1. 将给定的十进制数除以2,得到商和余数。 2. 将商再次除以2,得到新的商和余数。 3. 连续重复此过程,直到商为0为止。 4. 将每个余数从下到上排列,即可得到对应的二进制数。
- 步驟1:將十進制數除以2,寫下餘數並指定值 R1 = 餘數,同樣指定值 Q1 = 在此除法中獲得的商。
- 第2步:現在將Q1除以2並記下餘數。將餘數的值指定給R2並將商的值指定給Q1。
- 步驟3:繼續這個序列,直到在某個除法中得到商(Qn)等於0的值。
- 第四步:您可以將二進制數字寫成: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) 十进制 = (10110011) 二進制
如何將二進制和十進制數字系統中小數點後的數字進行轉換?
迄今為止,我們已經學會了如何在二進制和十進制之間轉換整數。那麼帶有小數位的數字呢?步驟與上面的步驟類似。首先,將數字分成小數點前後的部分。讓我們考慮一個十進制數字 1932.1875:
它由一个整数部分1932和小数部分0.1875组成。对于整数部分1932, 使用上面的步骤。得到的二进制等值为: 11110001100.
小數部分0.1875可以按照以下模式進行轉換。將小數部分乘以二,如果結果超過1,則寫下1,然後從結果中減去1。如果結果小於1,則寫下0。接著,繼續乘以二。否則,寫下0。
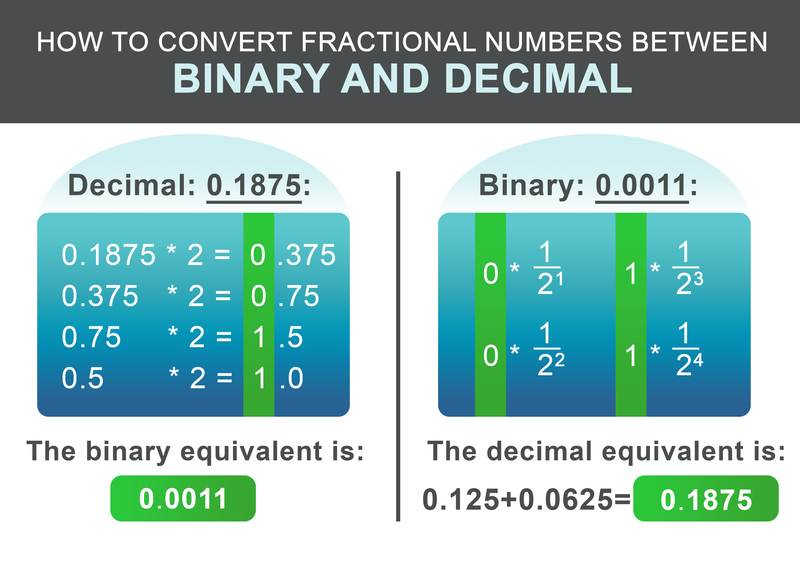
對於我們的例子0.1875,結果的二進制數是:0.0011在最後一步中將整數和小數部分相加:
$$11110001100.0011$$
將二進位小數轉換回去的方法更加簡單。將小數點後的每位數加上 $1/2^i$,其中 i 是從左到右的數位位置,從1開始。
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
二進位制度及其應用
一個數字系統是一系列不同的符號組合,每個符號都有特定的權重。數字系統的主要特徵是基數或底數,它定義了在特定數字系統中使用的符號總數。例如,二進制數字系統的基數是2,十進制數字系統的基數是10。
二進制系統的位元空間
在二进制系统中,我们有两个不同的数字:0和1。在计算机中,我们有像触发器这样的设备,可以根据控制信号存储任意两个电平中的任意一个。较高的电平被赋予值1,较低的电平被赋予值0,从而形成了一个二进制系统。
計算機中二進制系統的重要性:
一台電腦使用數以億計的數位電晶體進行操作。數位一詞與離散的邏輯電平有關。邏輯電平是指不同的電位,如5V、0V、10V等等。
任何一台電腦都是使用二進制邏輯運作,所以如果我們要表示電腦,我們必須使用基數為2的數字來進行計算。這個數字系統中的兩個符號類似於兩個離散的邏輯水平。為了方便起見,我們將這兩個符號分別表示為0和1,但在電腦中,0和1代表著不同的電壓水平。一般來說,0代表較低的電壓水平,而1代表著較高的電壓水平。
電腦螢幕上所看到的或透過滑鼠或鍵盤輸入的都是0和1,唯一的不同就是它們的順序排列。所以,如果我們想要透過電腦完成工作,我們必須了解二進制的運作方式,以及二進制與十進制的關係,進行數值的轉換到我們熟悉的領域中。
