
Comment convertir des nombres binaires en décimaux :
- Étape 1 : écrivez le poids associé à chaque chiffre du nombre binaire. Le poids est égal à 2 par la puissance de la position du chiffre dans le nombre lu de droite à gauche.
- Étape 2 : Notez maintenant le poids pour lequel la valeur binaire est égale à 1.
- Étape 3 : Additionnez tous les chiffres obtenus à l'étape précédente.
- Étape 4 : Le nombre obtenu à la dernière étape sera l'équivalent décimal du nombre binaire.
Considérons une valeur binaire 1101001.
1.) Première étape :
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Poids associé} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Deuxième étape : Poids pour lesquels les chiffres binaires sont 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Troisième étape : Additionner tous les poids
$$105 = 64 + 32 + 8 + 1$$
4.) Dernière étape : L'équivalent décimal du binaire est :: 105
Comment convertir des nombres décimaux en binaire :
En suivant ces étapes, vous pouvez convertir n'importe quel nombre décimal en système binaire :
- Étape 1 : Divisez le nombre décimal par 2 et notez le reste. Attribuez une valeur R1 = reste, de même que la valeur Q1 = quotient obtenu lors de cette division.
- Étape 2 : divisez maintenant Q1 par 2 et notez le reste. Attribuez la valeur du reste à R2 et la valeur du quotient à Q1.
- Étape 3 : Continuez la séquence jusqu'à ce qu'à un moment donné dans une division vous obteniez la valeur du quotient (Qn) égale à 0.
- Étape 4 : Vous pouvez écrire le nombre binaire comme suit : $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARY
Comment convertir les chiffres après la virgule entre le système numérique binaire et décimal ?
Jusqu'à présent, nous avons appris à convertir des nombres entiers entre binaire et décimal. Qu'en est-il des nombres avec des décimales ? La procédure est similaire aux étapes précédentes. Tout d'abord, divisez le nombre en sa partie avant et après la décimale. Considérons le nombre décimal 1932,1875 :
Elle est constituée d'une partie entière 1932 et de la fraction 0,1875. Pour la partie entière 1932, utilisez les étapes ci-dessus. L'équivalent binaire résultant est : 11110001100.
La partie fractionnaire 0,1875 peut être convertie selon le schéma suivant. Multipliez récursivement la partie fractionnaire par deux. Si le résultat est supérieur à 1, notez 1, puis soustrayez 1 du nombre obtenu. Si le résultat est inférieur à 1, notez 0. Ensuite, continuez à multiplier par deux. Sinon, notez 0.
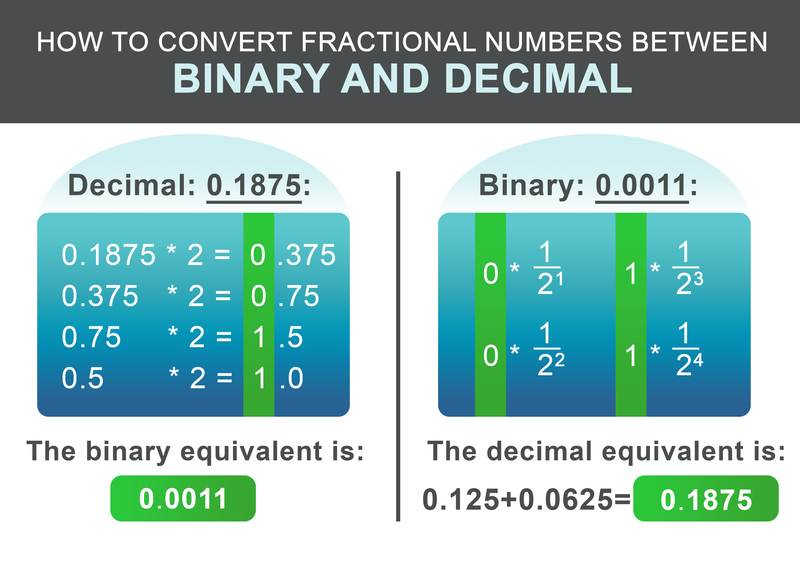
Pour notre exemple 0,1875, le nombre binaire résultant est : 0,0011 Dans la dernière étape, on ajoute les parties entières et fractionnaires :
$$11110001100.0011$$
Pour reconvertir la faction binaire, le processus est encore plus simple. Ajoutez $1/2^i$ pour chaque chiffre après le point au résultat, i étant la position du chiffre après de gauche à droite, en commençant par 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Le système de nombres binaires et ses applications
Un système numérique est un ensemble de différentes combinaisons de symboles, chaque symbole ayant un poids spécifique. Les principales caractéristiques d'un système numérique sont le radix ou la base qui définit le nombre total de symboles utilisés dans un système numérique particulier. Par exemple, le radix du système numérique binaire est 2, et le radix du système numérique décimal est 10.
L'espace numérique du système binaire
Dans le système binaire, nous avons deux chiffres distincts : 0 et 1 : Dans les ordinateurs, nous disposons de dispositifs tels que les bascules qui peuvent stocker l'un des deux niveaux en fonction d'un signal de commande. Le niveau supérieur se voit attribuer la valeur 1 et le niveau inférieur la valeur 0, formant ainsi un système binaire.
Importance du système binaire en informatique :
Un ordinateur utilise des milliards et des milliards de transistors qui fonctionnent de manière numérique. Le terme numérique concerne les niveaux logiques discrets. Les niveaux logiques sont les différents niveaux de potentiel comme 5V, 0V, 10V, et bien d'autres.
Tout ordinateur fonctionne selon une logique binaire, donc si nous voulons représenter l'ordinateur, nous devons écrire les nombres avec un radix égal à 2. Les deux symboles de ce système numérique sont analogues aux deux niveaux logiques discrets. Pour notre facilité, nous considérons que ces deux symboles sont 0 et 1, mais pour un ordinateur, 0 et 1 sont des niveaux de tension différents. En général, 0 est considéré comme le niveau de tension le plus bas et 1 est considéré comme le niveau de tension le plus élevé.
Tout ce que nous voyons sur l'écran de l'ordinateur ou ce que nous saisissons à l'aide d'une souris ou d'un clavier sont des 0 et des 1, la seule différence étant leur disposition séquentielle. Donc, si nous voulons faire notre travail à partir de l'ordinateur, nous devons savoir comment fonctionne le binaire et quelle est la relation entre le binaire et les décimales pour convertir les valeurs du domaine binaire dans notre domaine connu.
