
Como converter Números Binários em Decimal:
- Passo 1: Escreva o peso associado abaixo de cada dígito do número binário. O peso é 2 pela potência da posição do dígito na leitura do número da direita para a esquerda.
- Etapa 2: Agora note o peso para o qual o valor binário é igual a 1.
- Passo 3: Acrescentar todos os números obtidos no passo anterior
- Passo 4: O número do último passo será o equivalente decimal do número binário.
Consideremos um valor binário 1101001.
1.) Primeiro passo:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÁRIO} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Peso associado} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Segundo passo: Pesos para os quais os dígitos binários são 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Terceiro passo: Acrescentar todos os pesos
$$105 = 64 + 32 + 8 + 1$$
4.) Último passo: O equivalente Decimal do Binário é:: 105
Como converter números decimais em Binários:
Seguindo estes passos pode converter qualquer número decimal no sistema binário:
- Passo 1: Dividir o número decimal por 2 e escrever o restante e atribuir um valor R1 = restante, atribuindo de forma semelhante o valor Q1 = quociente obtido nesta divisão.
- Passo 2: Agora dividir Q1 com 2 e anotar o resto. Atribuir o valor do restante a R2 e o valor do quociente a Q1.
- Passo 3: Continuar a sequência até que em algum momento numa divisão se obtenha o valor do quociente (Qn) igual a 0.
- Passo 4: Pode escrever o número binário como: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINÁRIO
Como converter os dígitos após o ponto decimal entre o sistema numérico binário e decimal?
Até agora, aprendemos a converter números inteiros entre binário e decimal. Que tal números com casas decimais? O procedimento é semelhante aos passos acima indicados. Primeiro, dividir o número na sua parte antes e depois da casa decimal. Vamos considerar o número decimal 1932.1875:
É constituída por uma parte inteira de 1932 e a fracção 0,1875. Para a parte inteira de 1932, utilizar os passos de cima. O equivalente binário resultante é: 11110001100.
A parte fracionada 0,1875 pode ser convertida de acordo com o seguinte esquema. Multiplicar recursivamente a parte fraccionada por dois. Se o resultado exceder 1, escrever 1 e depois subtrair 1 ao número resultante. Se o resultado for inferior a 1, escrever 0. A seguir, continuar a multiplicar por dois. Caso contrário, anotar 0.
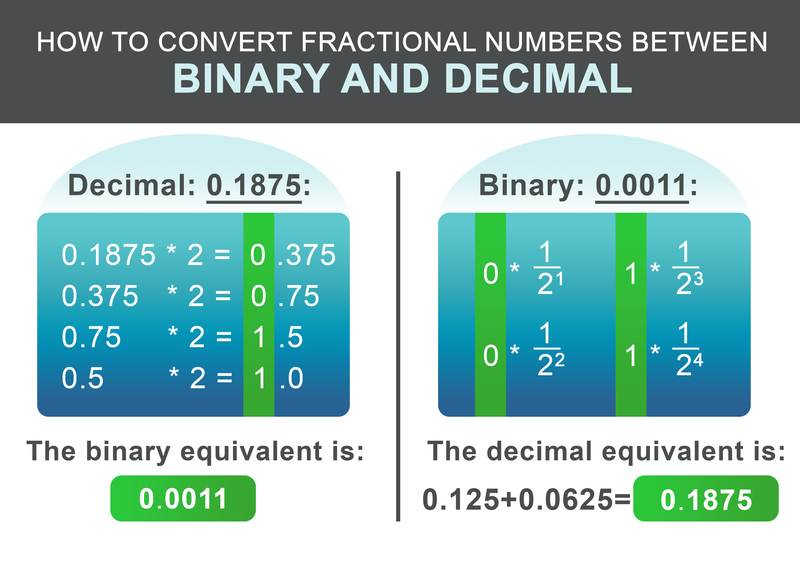
Para o nosso exemplo 0,1875, o número binário resultante é: 0,0011 No último passo, adicionar o número inteiro e as partes fracionárias:
$$11110001100.0011$$
Para a conversão da facção binária de volta, o fluxo de trabalho é ainda mais simples. Adicionar $1/2^i$ para cada dígito após o ponto ao resultado, sendo i a posição do dígito após da esquerda para a direita, começando em 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
O Sistema de Números Binários e as suas Aplicações
Um sistema numérico é um conjunto de diferentes combinações de símbolos, com cada símbolo com um peso específico. As principais características de um sistema numérico são o radix ou base que define o número total de símbolos utilizados num determinado sistema numérico. Por exemplo, o radix do sistema de número binário é 2, e o radix do sistema de número decimal é 10.
O Espaço do Dígito do Sistema Binário
No sistema binário, temos dois dígitos distintos: 0 e 1. nos computadores, temos dispositivos como flip-flops que podem armazenar qualquer um dos dois níveis de acordo com um sinal de controlo. Ao nível superior é atribuído o valor 1 e ao nível inferior é atribuído o valor 0, formando assim um sistema binário.
Importância do Sistema Binário na Computação:
Um computador faz uso de milhares de milhões e milhares de milhões de transístores que operam digitalmente. O termo digital preocupa-se com os níveis lógicos discretos. Os níveis lógicos são os diferentes níveis potenciais como 5V, 0V, 10v, e muitos outros.
Qualquer computador funciona utilizando uma lógica binária, portanto, se quisermos representar o computador, devemos escrever os números com radix igual a 2. Os dois símbolos neste sistema numérico são análogos aos dois níveis lógicos discretos. Para nossa facilidade, consideramos estes dois símbolos como 0 e 1, mas para um computador 0 e 1 são níveis de tensão diferentes. Geralmente, 0 é considerado para o nível de voltagem inferior e 1 é considerado para o nível de voltagem superior.
Tudo o que vemos no ecrã do computador ou fornecemos a entrada através de um rato ou teclado são todos 0s e 1s, a única diferença é a sua disposição sequencial. Portanto, se quisermos fazer o nosso trabalho a partir do computador, temos de saber como funciona o binário e qual é a relação do binário com casas decimais para converter os valores do domínio binário no nosso domínio conhecido.
