Enter Decimal OR Binary Number:
Result:
converting binary to decimal

Kā pārvērst bināros skaitļus uz decimālskaitli:

  • 1. solis: pierakstiet svaru, kas saistīts ar katru bināra skaitļa ciparu. Svars ir 2 ar cipara pozīcijas lielumu skaitlī, lasot no labās puses uz kreiso.
  • 2. solis: Tagad atzīmējiet svaru, kura bināra vērtība ir vienāda ar 1.
  • 3. solis: saskaitiet visus iepriekšējā solī iegūtos skaitļus.
  • 4. solis: Pēdējā solī iegūtais skaitlis būs binārā skaitļa decimālais ekvivalents.

Aplūkosim bināro vērtību 1101001.

1.) Pirmais solis:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Saistīts svars} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Otrais solis: Svariem, kuru binārajiem cipariem ir 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Trešais solis: Visu svaru saskaitīšana

$$105 = 64 + 32 + 8 + 1$$

4.) Pēdējais solis: Bināro kodu decimālais ekvivalents ir:: 105

Kā pārvērst decimālskaitļus uz bināro:

Veicot šos soļus, varat pārvērst jebkuru decimālo skaitli binārajā sistēmā:

  • 1. solis: daliet decimālskaitli ar 2, pierakstiet atlikumu un piešķiriet vērtību R1 = atlikums, līdzīgi piešķirot vērtību Q1 = šajā dalījumā iegūtais kvantients.
  • 2. solis: tagad daliet Q1 ar 2 un atzīmējiet atlikumu. Atlikuma vērtību piešķiriet R2, bet reizinātāja vērtību - Q1.
  • 3. solis: Turpiniet secību, līdz kādā dalīšanas punktā iegūstat kvantienta (Qn) vērtību, kas vienāda ar 0.
  • 4. solis: Bināro skaitli var ierakstīt kā: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
Piemērs: Apskatīsim decimālskaitli 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Tagad jūs varat pierakstīt bināro skaitli no atlikumiem, sākot ar R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINARY

Kā konvertēt ciparus aiz decimālpunkta starp bināro un decimālo skaitļu sistēmu?

Līdz šim mēs esam mācījušies, kā pārvērst veselos skaitļus no bināra un decimālskaitļa. Kā ir ar skaitļiem ar decimāldaļu? Procedūra ir līdzīga iepriekš minētajiem soļiem. Vispirms sadaliet skaitli tā daļā pirms un pēc decimāldaļas. Aplūkosim decimālskaitli 1932,1875:

To veido veselā skaitļa daļa 1932 un daļa 0,1875. Attiecībā uz veselā skaitļa daļu 1932 izmantojiet iepriekš aprakstītos soļus. Iegūtais binārais ekvivalents ir: 11110001100.

Daļskaitļa daļu 0,1875 var konvertēt saskaņā ar šādu shēmu. Rekursīvi reizina daļu ar divi. Ja rezultāts ir lielāks par 1, ierakstiet 1 un pēc tam atņemiet 1 no iegūtā skaitļa. Ja rezultāts ir mazāks par 1, ierakstiet 0. Tālāk turpiniet reizināt ar divi. Pretējā gadījumā ierakstiet 0.

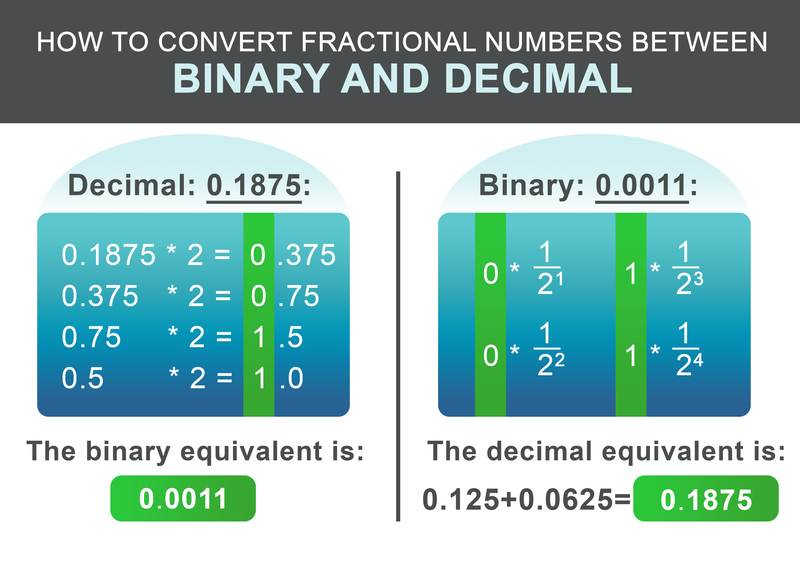
converting binary to decimal

Mūsu piemēram, 0,1875, iegūtais binārais skaitlis ir: 0,0011 Pēdējā solī saskaitiet veselos skaitļus un daļskaitļus:

$$11110001100.0011$$

Lai konvertētu bināro frakciju atpakaļ, darba process ir vēl vienkāršāks. Pievienojiet $1/2^i$ par katru ciparu pēc punkta rezultātam, kur i ir cipara pozīcija no kreisās uz labo pusi, sākot no 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Binārā skaitļu sistēma un tās lietojumi

Skaitļu sistēma ir dažādu simbolu kombināciju kopums, kur katram simbolam ir noteikts svars. Galvenās skaitļu sistēmas īpašības ir radikss jeb bāze, kas nosaka konkrētā skaitļu sistēmā izmantoto simbolu kopējo skaitu. Piemēram, bināro skaitļu sistēmas radikss ir 2, bet decimālās skaitļu sistēmas radikss ir 10.

Divējādinieku sistēmas ciparu telpa

Binārajā sistēmā ir divi dažādi cipari: Datoros ir tādas ierīces kā flip-flopi, kas var saglabāt jebkuru no šiem diviem līmeņiem saskaņā ar vadības signālu. Augstākajam līmenim tiek piešķirta vērtība 1, bet zemākajam līmenim tiek piešķirta vērtība 0, tādējādi veidojot bināro sistēmu.

Dinary sistēmas nozīme skaitļošanā:

Dators izmanto miljardiem un miljardiem tranzistoru, kas darbojas digitāli. Termins "digitālais" attiecas uz diskrētiem loģikas līmeņiem. Loģiskie līmeņi ir dažādi potenciālu līmeņi, piemēram, 5 V, 0 V, 10 V un daudzi citi.

Jebkurš dators darbojas, izmantojot bināro loģiku, tāpēc, ja vēlamies attēlot datoru, skaitļi ir jāraksta ar radikss vienādu ar 2. Divi simboli šajā skaitļu sistēmā ir analogi diviem diskrētās loģikas līmeņiem. Mūsu ērtībai mēs šos divus simbolus uzskatām par 0 un 1, bet datorā 0 un 1 ir dažādi sprieguma līmeņi. Parasti 0 tiek uzskatīts par zemāko sprieguma līmeni, bet 1 - par augstāko sprieguma līmeni.

Viss, ko mēs redzam datora ekrānā vai ievadām ar peli vai tastatūru, ir 0 un 1, vienīgā atšķirība ir to secīgais izkārtojums. Tātad, ja vēlamies, lai mūsu darbs tiktu veikts ar datoru, mums jāzina, kā darbojas binārais skaitlis un kāda ir bināro skaitļu saistība ar decimālskaitļiem, lai pārvērstu vērtības no bināra domēna mums zināmajā domēnā.