बाइनरी से दशमलव रूपांतरक: बाइनरी को दशमलव में और उसीप्रक्रिया के विपरीत रूपांतरक करता है।

---

बाइनरी संख्याओं को दशमलव में कैसे रूपांतरित करें:

• स्टेप 1: दर्ज करें बाइनरी संख्या में हर अंक के नीचे संबंधित वजन। वजन है 2 के गुण अंक की स्थिति का आधार होता है, जबकि अंक को दाईं ओर से बाईं ओर पढ़ते हैं।
• स्टेप 2: अब वजन को ध्यान से जोड़ें जिसका बाइनरी मान 1 के बराबर हो।
• स्टेप 3: पिछले स्टेप में प्राप्त किए गए सभी नंबरों को जोड़ें।
• चरण 4: पिछले स्टेप से प्राप्त संख्या बाइनरी संख्या के दशमलवीय समानांतर होगी।

चलो हम एक द्विआधारी मानय 1101001 का विचार करें।

पहला कदम:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{बाइनरी} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{वजन संबंधी} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) दूसरा कदम: जिन वजनों के बाइनरी अंक 1 हैं।

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) तीसरा कदम: सभी वज़नों को जोड़ना

$$105 = 64 + 32 + 8 + 1$$

4.) अंतिम कदम: द्विआदिक का दशमलव समकक्ष है:: 105

दशमलव संख्याओं को बाइनरी में कैसे बदलें:

इन चरणों का पालन करके आप किसी भी दशमलव संख्या को बाइनरी प्रणाली में परिवर्तित कर सकते हैं:

• स्टेप 1: दशमलव संख्या को 2 से भाग करें और शेष को लिखें और मान R1 = शेष करें, उसी प्रकार मान Q1 = इस विभाजन में प्राप्त भाग को सौपें।
• चरण 2: अब Q1 को 2 से विभाजित करें और शेष को ध्यान में रखें। शेष की मानता R2 को और वंश मत की मानता Q1 को आसान करें।
• स्टेप 3: विभाजन में किसी बिंदु तक अनुपात (Qn) का मान शून्य (0) के बराबर हो जाने तक अनुक्रम जारी रखें।
• चरण 4: आप बाइनरी संख्या इसप्रकार लिख सकते हैं: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

उदाहरण: हम दशमलव संख्या 179 को मान लेते हैं। \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} अब आप R8 के साथ बचे हुए संख्याओं से बाइनरी संख्या लिख सकते हैं: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) दशमलव = (10110011) बाइनरी

दशमलव बिनरी और दशमलव संख्या प्रणाली के बीच अंक रूपांतरित करेंगे, वह कैसे होगा?

अब तक, हमने इंटीजर संख्याओं को बाइनरी और डेसिमल के बीच परिवर्तित करने का तरीका सीखा है। दशमलव स्थान वाले संख्याओं के साथ क्या है? प्रक्रिया पहले वर्ग के साथ और दशमलव स्थान के बाद के हिस्से में संख्या को विभाजित करें। हम डेसिमल संख्या 1932.1875 को ध्यान में लेते हैं:

इसमें एक पूर्णांक भाग 1932 और भिन्न 0.1875 होता है। 1932 के लिए पूर्व दिए गए चरणों का उपयोग करें। परिणामस्वरूप बाइनरी समकक्ष है: 11110001100.

यदि हम 0.1875 को नकरीय भाग के रूप में बदलना चाहें, तो निम्नलिखित तरीके का पालन करें। नकरीय भाग को दो से गुणा करें।यदि परिणाम 1 से अधिक हो, तो 1 लिखें और परिणामी नंबर से 1 घटाएँ। यदि परिणाम एक से कम हो, तो 0 लिखें। अगले, दोबारा दो से गुणा करें। अन्यथा, 0 लिखें।

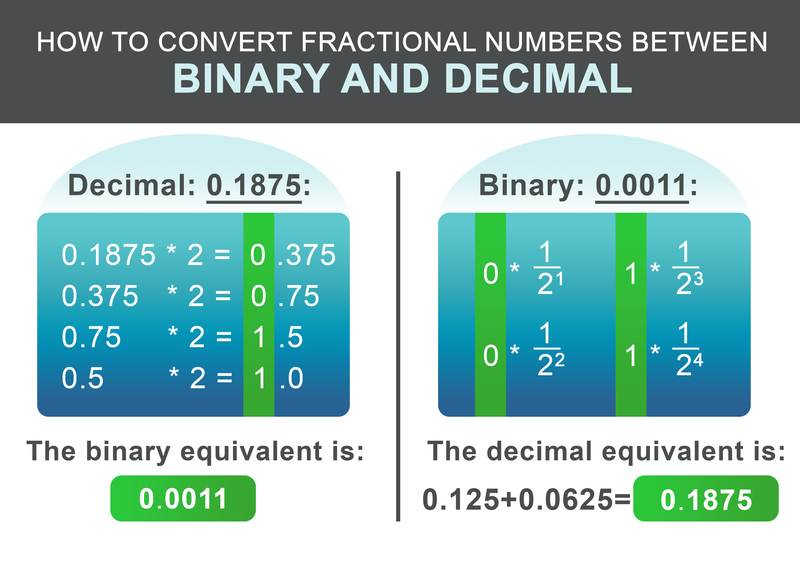
हमारी उदाहरण के लिए 0.1875, परिणामकारी बाइनरी संख्या है: 0.0011. अंतिम चरण में पूर्णांक और अंशिका भाग जोड़ें:

$$11110001100.0011$$

बाइनरी अंश को वापसी में परिवर्तित करने के लिए, यह प्रक्रिया भी और भी सरल है। परिणाम में नया dot डेसीमल अंश के बाद के प्रत्येक अंक के लिए $1/2^i$ जोड़ें, जहां i दिये गये अंक की होने की स्थानिकता होती है, बाएं से दायंन ओर, शुरू होकर 1 के रूप में।

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

द्विआधारी संख्या प्रणाली और उसके अनुप्रयोग

एक संख्या प्रणाली विभिन्न प्रतीकों के विभिन्न संयोजनों का एक सेट होती है, प्रत्येक प्रतीक का एक विशेष वजन होता है। एक संख्या प्रणाली की मुख्य विशेषताएं वे आधार हैं जिनसे कोई विशेष संख्या प्रणाली में प्रतीकों की कुल संख्या को निर्धारित की जाती है। उदाहरण के लिए, द्विआधारी संख्या प्रणाली का अंकशास्त्र 2 होता है और दशमलव संख्या प्रणाली का अंकशास्त्र 10 होता है।

बाइनरी सिस्टम के अंक स्थान

द्विआधारी प्रणाली में, हमारे पास दो अलग-अलग अंक होते हैं: 0 और 1. कंप्यूटर में, हमारे पास फ्लिप-फ्लॉप जैसी उपकरण होते हैं जो एक नियंत्रण सिग्नल के अनुसार इन दो स्तरों में से किसी एक का संग्रह कर सकते हैं। उच्च स्तर को 1 माना जाता है और निचले स्तर को 0 माना जाता है, इस प्रकार एक द्विआधारी प्रणाली बनाई जाती है।

कंप्यूटिंग में द्विआधारी प्रणाली का महत्व:

एक कंप्यूटर बिलियन्स और बिलियन्स ट्रांजिस्टर का उपयोग करता है जो डिजिटली संचालित होते हैं। डिजिटल का अर्थ विचरण तार्किक स्तरों के साथ जुड़ा होता है। तार्किक स्तर विभिन्न पॉटेंशियल स्तर हैं जैसे 5V, 0V, 10V और अन्य कई।

किसी भी कंप्यूटर बाइनरी तार्किक का उपयोग करके करता है, इसलिए अगर हम कंप्यूटर को प्रतिष्ठित करना चाहते हैं, तो हमें यहां द्विंद्रीयांक प्रतिष्ठित करना होगा। इस संख्या प्रणाली में दो प्रतिष्ठित तार्किक स्तरों के सबंध में होते हैं। हमारी सुविधा के लिए, हम इन दो प्रतीकों को 0 और 1 के रूप में मान्य करते हैं, लेकिन कंप्यूटर के लिए 0 और 1 अलग वोल्टेज स्तर होते हैं। आमतौर पर, 0 को निचले वोल्टेज स्तर के लिए मान्य किया जाता है और 1 को उच्च वोल्टेज स्तर के लिए मान्य किया जाता है।

सभी हम कंप्यूटर की स्क्रीन पर देखते हैं या माउस या कीबोर्ड के माध्यम से इनपुट प्रदान करते हैं, सभी 0 और 1 हैं, एकमात्र अंतर उनके क्रमिक व्यवस्था में होता है। इसलिए, अगर हम कंप्यूटर से अपना काम करवाना चाहते हैं, तो हमें यह जानना चाहिए कि बाइनरी कैसे काम करता है और बाइनरी का दशमलव के साथ क्या संबंध है ताकि हम बाइनरी डोमेन से मान्य डोमेन में मानों को रूपांतरित कर सकें।