İkili - Ondalık Dönüştürücü: İkiliyi ondalık sayıya veya tam tersine dönüştürür.

---

İkili Sayıları Ondalık Sayıya Dönüştürme:

• Adım 1: İkili sayının her basamağının altına ilişkili ağırlığı yazın. Ağırlık, sağdan sola doğru okunan sayıdaki rakamın konumunun gücü ile 2'dir.
• Adım 2: Şimdi ikili değerin 1'e eşit olduğu ağırlığı not edin.
• Adım 3: Önceki adımda elde edilen tüm sayıları toplayın
• Adım 4: Son adımdaki sayı, ikili sayının ondalık karşılığı olacaktır.

İkili bir değer olan 1101001'i ele alalım.

1.) İlk adım:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{İKİLİ} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Ağırlık ile ilişkili} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) İkinci adım: İkili basamakları 1 olan ağırlıklar.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Üçüncü adım: Tüm ağırlıkların toplanması

$$105 = 64 + 32 + 8 + 1$$

4.) Son adım: Binary'nin Decimal karşılığı şudur:: 105

Ondalık Sayıları İkiliye Dönüştürme:

Bu adımları izleyerek herhangi bir ondalık sayıyı ikili sisteme dönüştürebilirsiniz:

• Adım 1: Ondalık sayıyı 2'ye bölün ve kalanı yazın ve bir R1 = kalan değeri atayın, benzer şekilde bu bölme işleminde elde edilen Q1 = bölüm değerini atayın.
• Adım 2: Şimdi Q1'i 2'ye bölün ve kalanı not edin. Kalanın değerini R2'ye ve bölümün değerini Q1'e atayın.
• Adım 3: Bölme işleminin bir noktasında bölümün (Qn) değeri 0'a eşit olana kadar diziye devam edin.
• Adım 4: İkili sayıyı şu şekilde yazabilirsiniz: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Örnek: Ondalık sayı 179'u ele alalım. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Şimdi R8 ile başlayarak kalanlardan ikili sayıyı yazabilirsiniz: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) İKİLİ

Ondalık noktadan sonraki rakamları ikili ve ondalık sayı sistemi arasında nasıl dönüştürürsünüz?

Şimdiye kadar, tam sayıları ikili ve ondalık sayılar arasında nasıl dönüştüreceğimizi öğrendik. Peki ya ondalık basamaklı sayılar? Prosedür yukarıdaki adımlara benzer. İlk olarak, sayıyı ondalık basamaktan önceki ve sonraki kısımlarına ayırın. Ondalık sayı 1932.1875'i ele alalım:

Bir tamsayı parçası 1932 ve 0,1875 kesrinden oluşur. Tam sayı kısmı 1932 için yukarıdaki adımları kullanın. Ortaya çıkan ikili eşdeğer şudur: 11110001100.

Kesirli kısım 0.1875 aşağıdaki şemaya göre dönüştürülebilir. Yinelemeli olarak kesirli kısmı iki ile çarpın. Sonuç 1'i aşarsa, 1 yazın ve ardından elde edilen sayıdan 1 çıkarın. Sonuç birden küçükse 0 yazın. Sonra, iki ile çarpmaya devam edin. Aksi takdirde 0 yazın.

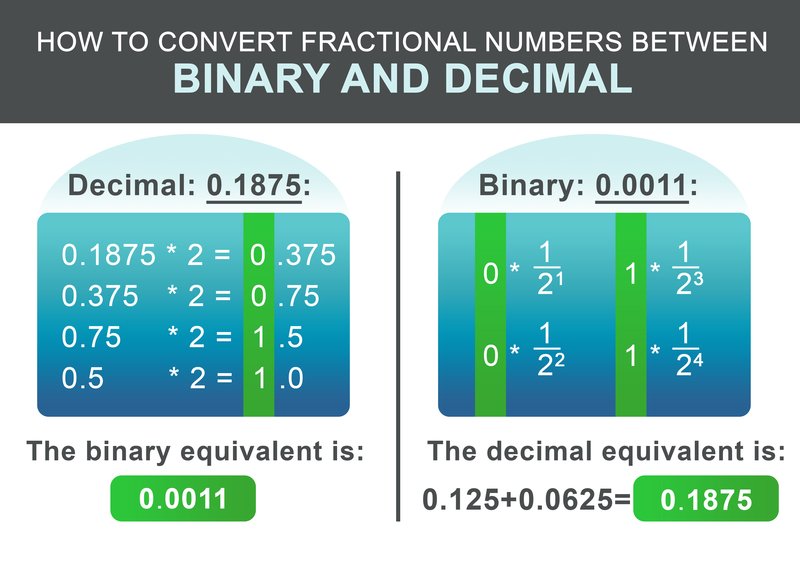
Örneğimiz için 0.1875, elde edilen ikili sayı: 0.0011 Son adımda tamsayı ve kesirli kısımları ekleyin:

$$11110001100.0011$$

İkili fraksiyonu geri dönüştürmek için iş akışı daha da basittir. Noktadan sonraki her rakam için sonuca $1/2^i$ ekleyin, burada i, 1'den başlayarak soldan sağa doğru sonraki rakamın konumudur.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

İkili Sayı Sistemi ve Uygulamaları

Bir sayı sistemi, her bir sembolün belirli bir ağırlığa sahip olduğu farklı sembol kombinasyonlarından oluşan bir kümedir. Bir sayı sisteminin temel özellikleri, belirli bir sayı sisteminde kullanılan toplam sembol sayısını tanımlayan radiks veya tabandır. Örneğin, ikili sayı sisteminin radiksi 2'dir ve ondalık sayı sisteminin radiksi 10'dur.

İkili Sistemin Rakam Uzayı

İkili sistemde, iki farklı rakamımız vardır: 0 ve 1. Bilgisayarlarda, bir kontrol sinyaline göre iki seviyeden herhangi birini saklayabilen flip-flop gibi cihazlarımız vardır. Daha yüksek seviyeye 1 değeri atanır ve daha düşük seviyeye 0 değeri atanır, böylece ikili bir sistem oluşturur.

Bilgi İşlemde İkili Sistemin Önemi:

Bir bilgisayar, dijital olarak çalışan milyarlarca ve milyarlarca transistörden yararlanır. Dijital terimi ayrık mantık seviyeleri ile ilgilidir. Mantık seviyeleri 5V, 0V, 10v ve diğerleri gibi farklı potansiyel seviyelerdir.

Herhangi bir bilgisayar ikili mantık kullanarak çalışır, bu nedenle bilgisayarı temsil etmek istiyorsak, sayıları 2'ye eşit radix ile yazmalıyız. Bu sayı sistemindeki iki sembol, iki ayrık mantık seviyesine benzer. Bize kolaylık sağlaması için bu iki sembolü 0 ve 1 olarak düşünüyoruz, ancak bir bilgisayar için 0 ve 1 farklı voltaj seviyeleridir. Genel olarak, 0 düşük voltaj seviyesi için ve 1 yüksek voltaj seviyesi için kabul edilir.

Bilgisayar ekranında gördüğümüz ya da bir fare veya klavye aracılığıyla girdi sağladığımız her şey 0'lar ve 1'lerdir, tek fark bunların sıralı dizilişidir. Bu nedenle, bilgisayarda işimizi halletmek istiyorsak, ikilinin nasıl çalıştığını ve değerleri ikili alandan bildiğimiz alana dönüştürmek için ikilinin ondalıklarla ilişkisinin ne olduğunu bilmeliyiz.