ตัวแปลงไบนารีเป็นทศนิยม: แปลงไบนารีเป็นทศนิยมและทำการกลับกัน

---

วิธีแปลงจำนวนฐานสองเป็นฐานสิบ:

• ขั้นตอนที่ 1: เขียนน้ำหนักที่เกี่ยวข้องใต้ทุกหลักของเลขฐานสอง น้ำหนักคือ 2 ในทศนิยมของตำแหน่งของหลักในการอ่านจากขวาไปซ้าย
• ขั้นตอนที่ 2: ตอนนี้บันทึกน้ำหนักสำหรับน้ำหนักที่มีค่าสอง進制เท่ากับ 1
• Step 3: บวกเลขทั้งหมดที่ได้จากขั้นตอนก่อนหน้านี้
• ขั้นตอนที่ 4: ตัวเลขจากขั้นตอนล่าสุดจะเป็นค่าทศนิยมที่เทียบเท่ากับตัวเลขฐานสอง

เรามาพิจารณาค่าทวนสอง 1101001

1.) ขั้นตอนแรก:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{ไบนารี } & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{น้ำหนักร่วม } & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) ขั้นตอนที่สอง: น้ำหนักร่วมกันสำหรับเลขฐานสองที่เท่ากับ 1

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) ขั้นตอนที่สาม: เพิ่มน้ำหนักทั้งหมด

$$105 = 64 + 32 + 8 + 1$$

4.) ขั้นตอนสุดท้าย: ทศนิยมที่เทียบเท่ากับระบบฐานสองคือ: : 105

วิธีแปลงจากเลขฐานสิบเทียบเป็นเลขฐานสอง:

โดยทำตามขั้นตอนเหล่านี้ คุณสามารถแปลงจำนวนทศนิยมใด ๆ เป็นระบบทวิภาคี:

• ขั้นตอนที่ 1: หารจำนวนทศนิยมด้วย 2 แล้วเขียนผลลัพธ์ที่เหลือและกำหนดค่า R1 = ผลหารเหลือ, โดยกำหนดค่า Q1 = ผลหารที่ได้จากการหารนี้
• ขั้นตอนที่ 2: แบ่ง Q1 ด้วย 2 แล้วจดเศษที่เหลือ กำหนดค่าเศษที่เหลือให้เป็น R2 และค่าส่วนหารให้เป็น Q1
• ขั้นตอนที่ 3: ซ้ำลำดับไปเรื่อยๆ จนกว่าที่จะได้ค่าของเศษ (Qn) ที่เท่ากับ 0 ในการหาร
• ขั้นตอนที่ 4: คุณสามารถเขียนตัวเลขฐานสองเป็น: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

ตัวอย่าง: ให้พิจารณาจำนวนทศนิยมฐานสิบ 179 \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} ตอนนี้คุณสามารถเขียนเลขฐานสองจากเศษที่เหลือลงบนกระดาษ โดยเริ่มต้นที่ R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) ทศนิยม = (10110011) ไบนารี

คุณแปลงหลักทศนิยมหลังจากจุดทศนิยมระหว่างระบบเลขฐานสองและตัวเลขทศนิยมได้อย่างไร?

จนถึงตอนนี้เราได้เรียนรู้วิธีการแปลงจำนวนเต็มระหว่างฐานสองและสิบ จะเป็นอย่างไรกับจำนวนที่มีจุดทศนิยม? กระบวนการนั้นคล้ายกับขั้นตอนที่กล่าวมาข้างต้น ก่อนอื่นให้แยกจำนวนออกเป็นส่วนของจำนวนนั้น ๆ ก่อนและหลังจุดทศนิยม มาลองพิจารณาจำนวนทศนิยม 1932.1875:

มันประกอบด้วยส่วนจำนวนเต็ม 1932 และส่วนเสริม 0.1875 สำหรับส่วนจำนวนเต็ม 1932 ใช้ขั้นตอนจากด้านบน ผลลัพธ์ที่ได้คือเทียบเท่าทางคณิตศาสตร์คือ: 11110001100

ส่วนเศษ 0.1875 สามารถแปลงตามแผนผังต่อไปนี้

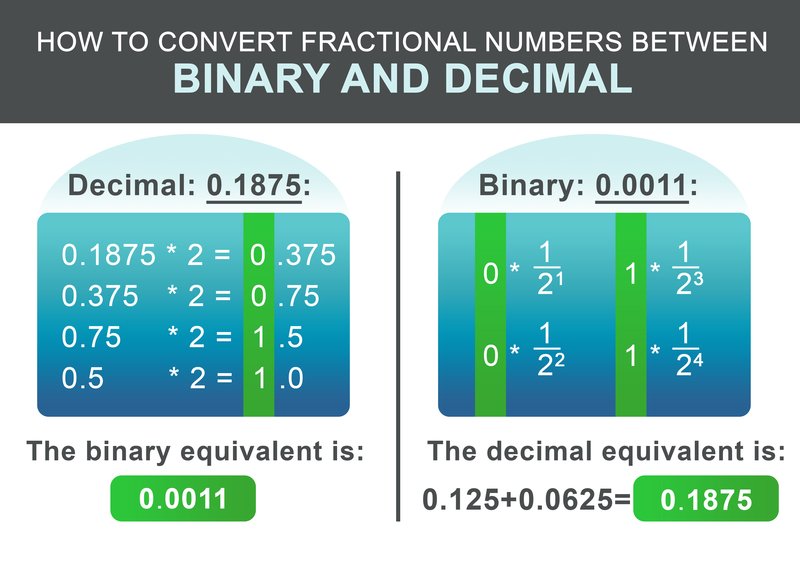
สำหรับตัวอย่างของเรา 0.1875 จำนวนทวีคูณทางสิบจะได้: 0.0011 ในขั้นตอนสุดท้ายให้เพิ่มส่วนจำนวนเต็มและส่วนปฏิทิน

$$11110001100.0011$$

สำหรับการแปลงเศษสิบจำนวนสองคู่กลับไป ขั้นตอนการทำงานง่ายยิ่งขึ้น เพิ่ม $1/2^i$ สำหรับทุกๆ หลักหลังจากจุดทศนิยมไปยังผลลัพธ์ โดยที่ i คือตำแหน่งของหลักหลังจากด้านซ้ายไปยังด้านขวา เริ่มต้นที่ 1

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

ระบบตัวเลขไบนารีและการใช้งานของมัน

ระบบจำนวนเป็นเซตของการผสมผสานสัญลักษณ์ที่แตกต่างกัน โดยที่แต่ละสัญลักษณ์มีน้ำหนักที่เฉพาะเจาะจง ลักษณะหลักของระบบจำนวนคือ radix หรือฐานที่กำหนดจำนวนสัญลักษณ์ทั้งหมดที่ใช้ในระบบจำนวนนั้น ตัวอย่างเช่น radix ของระบบจำนวนทวิภาคคือ 2 และ radix ของระบบจำนวนทศนิยมคือ 10

พื้นที่ของตัวเลขในระบบทวิภาค

ในระบบทวิภาคี จะมีตัวเลขสองตัวที่แตกต่างกัน: 0 และ 1 ในคอมพิวเตอร์ เรามีอุปกรณ์เช่นตัวล็อกที่สามารถเก็บข้อมูลในทั้งสองระดับได้ตามสัญญาณควบคุม ระดับที่สูงกำหนดค่าเท่ากับ 1 และระดับต่ำกำหนดค่าเท่ากับ 0 ดังนั้นจึงเกิดระบบทวิภาคี

ความสำคัญของระบบทวิภาคในการคำนวณ:

คอมพิวเตอร์ใช้พันล้าน พันล้านตัวจับกระแสที่ทำงานดิจิทัล คำว่าดิจิทัลเกี่ยวข้องกับระดับตรรกะที่ไม่ซึ่งซ้อนทับกัน ระดับตรรกะคือระดับศักย์ศูนย์ศักย์เป็นระดับที่ต่างๆ เช่น 5V, 0V, 10v และอีกมากมาย

คอมพิวเตอร์ทุกเครื่องทำงานโดยใช้ตรรกบิณฑิตฐานสอง ดังนั้นหากเราต้องการแทนที่คอมพิวเตอร์ เราต้องเขียนเลขที่มีฐานเท่ากับ 2 สัญลักษณ์สองอย่างในระบบเลขนี้คือคล้ายกับสองระดับตรรกะที่แตกต่างกัน สำหรับความสะดวกของเรา เราพิจารณาสัญลักษณ์สองอย่างนี้เป็น 0 และ 1 แต่สำหรับคอมพิวเตอร์ 0 และ 1 คือระดับแรงดันไฟฟ้าที่แตกต่างกัน โดยทั่วไป 0 ถือว่าเป็นระดับแรงดันไฟฟ้าต่ำกว่าและ 1 ถือว่าเป็นระดับแรงดันไฟฟ้าที่สูงกว่า

ที่เราเห็นบนหน้าจอคอมพิวเตอร์ หรือให้ป้อนข้อมูลผ่านเมาส์หรือคีย์บอร์ด คือ 0 และ 1 เท่านั้น แตกต่างกันก็คือการจัดลำดับตามลำดับที่แตกต่างกัน ดังนั้น ถ้าเราต้องการให้คอมพิวเตอร์ทำงานให้เสร็จ เราต้องรู้ว่าการเลขฐานสองทำงานอย่างไร และว่าการเลขฐานสองกับทศนิยมมีความสัมพันธ์อย่างไร เพื่อที่จะแปลงค่าจากโดเมนที่เลขฐานสองมายังโดเมนที่รู้จัก