Enter Decimal OR Binary Number:
Result:
converting binary to decimal

Kaip konvertuoti dvejetainius skaičius į dešimtainius:

  • 1 veiksmas: užrašykite po kiekvienu dvejetainio skaičiaus skaitmeniu esantį svorį. Svoris yra 2 pagal skaitmens padėties skaičiuje, skaitant iš dešinės į kairę, galybę.
  • 2 veiksmas: dabar pažymėkite svorį, kurio dvejetainė vertė lygi 1.
  • 3 veiksmas: Sudėkite visus ankstesniame žingsnyje gautus skaičius.
  • 4 veiksmas: paskutiniame veiksme gautas skaičius bus dvejetainio skaičiaus dešimtainis ekvivalentas.

Panagrinėkime dvejetainę reikšmę 1101001.

1.) Pirmas žingsnis:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Susijęs svoris} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Antrasis žingsnis: Svoriai, kurių dvejetainiai skaitmenys yra 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Trečiasis žingsnis: Visų svorių sudėjimas

$$105 = 64 + 32 + 8 + 1$$

4.) Paskutinis žingsnis: Dešimtainis dvejetainio skaičiaus atitikmuo yra:: 105

Kaip konvertuoti dešimtainius skaičius į dvejetainius:

Atlikę šiuos veiksmus, galite konvertuoti bet kokį dešimtainį skaičių į dvejetainę sistemą:

  • 1 veiksmas: padalykite dešimtainį skaičių iš 2, užrašykite likutį ir priskirkite reikšmę R1 = likutis, panašiai priskirdami reikšmę Q1 = dalijant gautas koeficientas.
  • 2 veiksmas: dabar padalykite Q1 iš 2 ir pasižymėkite likutį. Likutį priskirkite R2, o kvotos reikšmę - Q1.
  • 3 veiksmas: Tęskite seką, kol tam tikrame dalijimo taške gausite kvanto (Qn) reikšmę, lygią 0.
  • 4 žingsnis: dvejetainį skaičių galite užrašyti taip: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
Pavyzdys: Panagrinėkime dešimtainį skaičių 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Dabar galite užrašyti dvejetainį skaičių iš liekanų, pradedant nuo R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMALINIS = (10110011) BINARY

Kaip konvertuoti skaitmenis po dešimtainio taško tarp dvejetainės ir dešimtainės skaitmenų sistemos?

Iki šiol mokėmės, kaip paversti sveikuosius skaičius dvejetainiais ir dešimtainiais skaičiais. O kaip dėl skaičių su dešimtainėmis dalimis? Procedūra panaši į pirmiau aprašytus veiksmus. Pirmiausia padalykite skaičių į dalį prieš ir po dešimtainio skaičiaus. Panagrinėkime dešimtainį skaičių 1932,1875:

Jį sudaro sveikasis skaičius 1932 ir trupmena 0,1875. Viso skaičiaus daliai 1932 naudokite pirmiau pateiktus veiksmus. Gautas dvejetainis ekvivalentas yra: 11110001100.

Dalis 0,1875 gali būti konvertuojama pagal šią schemą. Rekursyviai padauginkite trupmeninę dalį iš dviejų. Jei rezultatas didesnis už 1, užrašykite 1 ir iš gauto skaičiaus atimkite 1. Jei rezultatas mažesnis už vienetą, užrašykite 0. Tada toliau dauginkite iš dviejų. Priešingu atveju užrašykite 0.

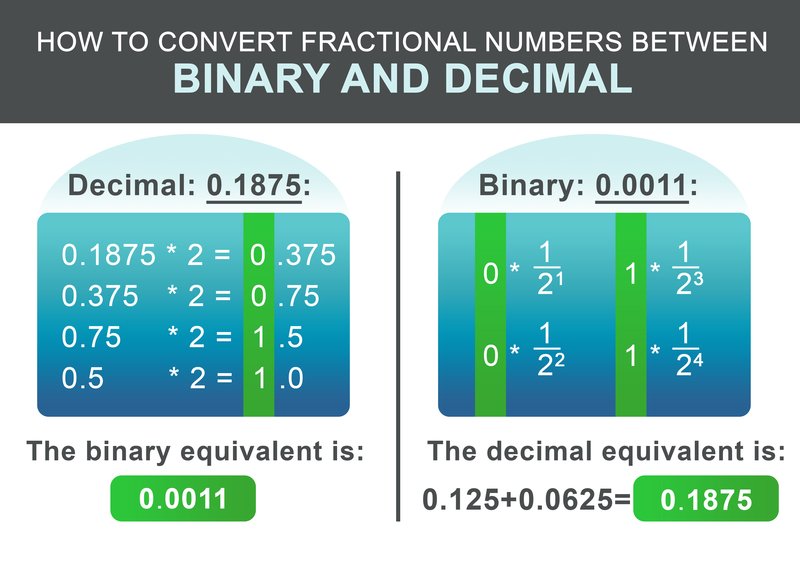
converting binary to decimal

Mūsų pavyzdžio 0,1875 atveju gautas dvejetainis skaičius yra: 0,0011 Paskutiniame žingsnyje sudėkite sveikąją ir trupmeninę dalis:

$$11110001100.0011$$

Dvejetainės frakcijos konvertavimo atgal darbo eiga yra dar paprastesnė. Prie rezultato pridėkite $1/2^i$ už kiekvieną skaitmenį po taško, kur i yra skaitmens po taško padėtis iš kairės į dešinę, pradedant nuo 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Dvejetainė skaičių sistema ir jos taikymas

Skaičių sistema - tai įvairių simbolių kombinacijų rinkinys, kuriame kiekvienas simbolis turi tam tikrą svorį. Pagrindinės skaičių sistemos savybės yra radiksas arba bazė, kuri apibrėžia bendrą konkrečioje skaičių sistemoje naudojamų simbolių skaičių. Pavyzdžiui, dvejetainės skaičių sistemos radiksas yra 2, o dešimtainės skaičių sistemos radiksas yra 10.

Dvejetainės sistemos skaitmenų erdvė

Dvejetainėje sistemoje yra du skirtingi skaitmenys: Kompiuteriuose turime tokius įtaisus kaip flip-flopai, kurie pagal valdymo signalą gali saugoti bet kurį iš dviejų lygių. Aukštesniam lygiui priskiriama reikšmė 1, o žemesniam lygiui - 0, todėl sudaroma dvejetainė sistema.

Dvejetainės sistemos svarba kompiuterijoje:

Kompiuteryje naudojami milijardai ir milijardai tranzistorių, kurie veikia skaitmeniniu būdu. Skaitmeninis terminas susijęs su diskrečiaisiais loginiais lygiais. Loginiai lygiai - tai skirtingi potencialų lygiai, pavyzdžiui, 5 V, 0 V, 10 V ir daugelis kitų.

Bet kuris kompiuteris veikia naudodamas dvejetainę logiką, todėl jei norime pavaizduoti kompiuterį, turime užrašyti skaičius, kurių radiksas lygus 2. Du šios skaičių sistemos simboliai yra analogiški dviem diskretiesiems loginiams lygiams. Kad būtų paprasčiau, šiuos du simbolius laikome 0 ir 1, tačiau kompiuteryje 0 ir 1 yra skirtingi įtampos lygiai. Paprastai 0 laikomas žemesniuoju įtampos lygiu, o 1 - aukštesniuoju įtampos lygiu.

Viskas, ką matome kompiuterio ekrane arba įvedame pelės ar klaviatūros pagalba, yra 0 ir 1, skiriasi tik jų eiliškumas. Taigi, jei norime atlikti darbą kompiuteriu, turime žinoti, kaip veikia dvejetainė sistema ir koks yra dvejetainės sistemos santykis su dešimtainiais skaičiais, kad galėtume konvertuoti dvejetainės srities reikšmes į mums žinomą sritį.