Enter Decimal OR Binary Number:
Result:
converting binary to decimal

Kuidas teisendada binaararvud kümnendarvudeks:

  • 1. samm: kirjutage iga binaararvu numbri all olev kaal. Kaal on 2, mis on numbri positsiooni potentsile vastavas numbris, lugedes seda paremalt vasakule.
  • 2. samm: Nüüd märkige kaal, mille binaarväärtus on võrdne 1.
  • 3. samm: liidetakse kõik eelmises etapis saadud arvud.
  • 4. samm: Viimase sammu number on binaarse arvu kümnendsüsteemi ekvivalent.

Vaatleme binaarset väärtust 1101001.

1.) Esimene samm:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Kaaluga seotud} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Teine samm: Kaalud, mille binaarsed numbrid on 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Kolmas samm: Kõikide kaalude lisamine

$$105 = 64 + 32 + 8 + 1$$

4.) Viimane samm: Detsimaalne ekvivalent Binary on:: 105

Kuidas teisendada kümnendarvud binaarseks:

Neid samme järgides saate teisendada mis tahes kümnendarvu binaarsüsteemi:

  • 1. samm: jagage kümnendarv 2ga ja kirjutage üles jääk ning määrake väärtus R1 = jääk, määrates samamoodi väärtuse Q1 = selle jagamisel saadud kvoot.
  • 2. samm: Nüüd jagage Q1 2-ga ja märkige jääk. Määrake jäägi väärtus R2-le ja korrutise väärtus Q1-le.
  • 3. samm: Jätkake jada, kuni mingis punktis jagamisel saad kvootori (Qn) väärtuseks 0.
  • 4. samm: Binaarset arvu saab kirjutada järgmiselt: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
Näide: Vaatleme kümnendarvu 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Nüüd võite kirjutada binaarvõrrandist jäägi, alustades R8-ga: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINARY

Kuidas teisendada numbreid pärast kümnendmärki kahe- ja kümnendsüsteemi vahel?

Siiani oleme õppinud, kuidas teisendada täisarvusid binaar- ja kümnendarvude vahel. Kuidas on lood kümnendkohtadega arvudega? Protseduur on sarnane ülaltoodud sammudega. Kõigepealt jagage arv kümnendkohtadele eelnevaks ja järgnevaks osaks. Vaatleme kümnendarvu 1932,1875:

See koosneb täisarvulisest osast 1932 ja murdarvust 0,1875. Tervikuosa 1932 puhul kasutage eespool kirjeldatud samme. Saadud binaarne ekvivalent on: 11110001100.

Murdosa 0,1875 saab teisendada vastavalt järgmisele skeemile. Korrutavalt korrutatakse murdosa kahega. Kui tulemus on suurem kui 1, kirjutatakse üles 1 ja seejärel lahutatakse saadud arvust 1. Kui tulemus on väiksem kui 1, kirjutatakse üles 0. Seejärel jätkatakse korrutamist kahega. Vastasel juhul kirjutatakse üles 0.

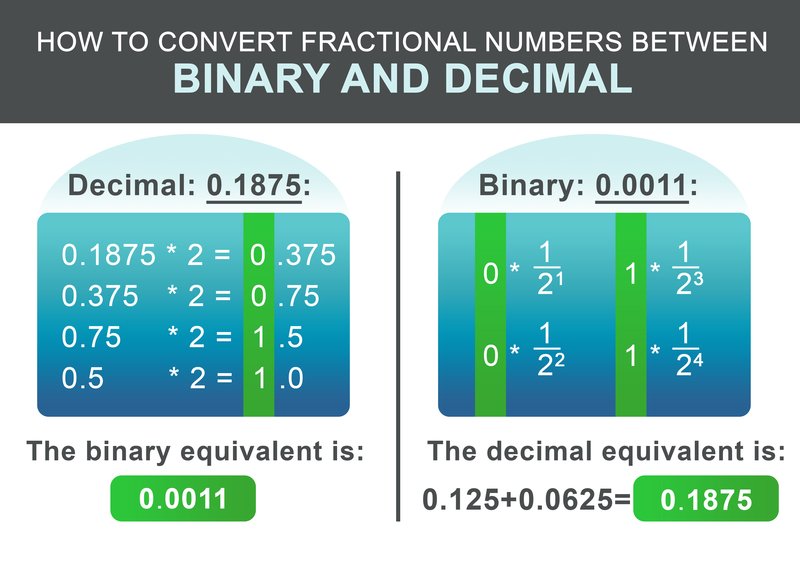
converting binary to decimal

Meie näite 0,1875 puhul on saadud binaarvõrrandiks: 0,0011 Viimases etapis liidetakse täisarvu ja murdosa:

$$11110001100.0011$$

Binaarse fraktsiooni tagasi teisendamiseks on tööprotsess veelgi lihtsam. Lisage tulemusele $1/2^i$ iga punktile järgneva numbri kohta, kusjuures i on numbri positsioon pärast vasakult paremale, alustades 1-st.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Binaararvude süsteem ja selle rakendused

Numbrisüsteem on sümbolite erinevate kombinatsioonide kogum, kusjuures igal sümbolil on kindel kaal. Numbrisüsteemi peamised omadused on radix või alus, mis määrab konkreetses numbrisüsteemis kasutatavate sümbolite koguarvu. Näiteks on binaarse arvusüsteemi radix 2 ja kümnendsüsteemi radix 10.

Binaarsüsteemi numbriruum

Binaarsüsteemis on meil kaks erinevat numbrit: Arvutites on meil sellised seadmed nagu flip-flopid, mis võivad salvestada ükskõik millise kahest tasemest vastavalt kontrollsignaalile. Kõrgemale tasemele antakse väärtus 1 ja madalamale tasemele väärtus 0, moodustades seega binaarsüsteemi.

Binaarsüsteemi tähtsus arvutustehnoloogias:

Arvuti kasutab miljardeid ja miljardeid transistoreid, mis töötavad digitaalselt. Mõiste "digitaalne" on seotud diskreetsete loogikatasanditega. Loogikatasemed on erinevad potentsiaalsed tasemed nagu 5V, 0V, 10v ja paljud teised.

Iga arvuti töötab binaarse loogika abil, nii et kui me tahame kujutada arvutit, peame kirjutama arvud radixiga 2. Kaks sümbolit selles arvusüsteemis on analoogilised kahe diskreetse loogikatasandiga. Meie lihtsuse huvides käsitleme neid kahte sümbolit kui 0 ja 1, kuid arvuti jaoks on 0 ja 1 erinevad pingetasemed. Üldiselt loetakse 0 madalamaks pingetasemeks ja 1 kõrgemaks pingetasemeks.

Kõik, mida me näeme arvuti ekraanil või anname sisendi hiire või klaviatuuri kaudu, on kõik 0-d ja 1-d. Ainus erinevus on nende järjestikune paigutus. Seega, kui me tahame arvutist oma tööd teha, peame teadma, kuidas binaarsus töötab ja milline on binaarsuse suhe kümnendkohtadega, et teisendada väärtused binaarsest domeenist meie teadaolevasse domeeni.