
바이너리 숫자를 십진수로 변환하는 방법:
- 1단계: 이진수의 각 자릿수 아래에 해당하는 가중치를 기록하세요. 가중치는 숫자의 오른쪽부터 읽을 때 자릿수의 위치에 따라 2의 거듭제곱으로 계산됩니다.
- 단계 2: 이제 이진 값이 1과 같은 무게를 기록하세요.
- 단계 3: 이전 단계에서 얻은 모든 숫자를 더하세요.
- 4단계: 이전 단계에서 얻은 숫자는 이진수의 십진수 변환값이 됩니다.
1101001 이진값 1101001을 고려해 봅시다.
1.) 첫 번째 단계:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{바이너리} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{가중치 관련} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) 두 번째 단계 : 이진 숫자가 1인 가중치들.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) 제3단계: 모든 가중치를 더하기
$$105 = 64 + 32 + 8 + 1$$
4.) 마지막 단계: 이진수의 십진수 형식은: : 105
소수점 숫자를 2진수로 변환하는 방법:
이 단계에 따라서 어떤 십진수든 이진법으로 변환할 수 있습니다:
- 단계 1: 소수점 숫자를 2로 나누고 나머지를 기록하고 나눗셈으로 얻은 몫을 값 R1로 할당하고 값 Q1로 할당합니다.
- 2단계: 이제 Q1을 2로 나누고 나머지를 기록하세요. 나머지의 값을 R2에 할당하고 몫의 값을 Q1에 할당하세요.
- 단계 3: 몫(Qn)이 0이 되는 분할 지점까지 일련의 과정을 계속 진행하세요.
- 단계 4: 이진 수를 다음과 같이 쓸 수 있습니다: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) 바이너리
소수점 이하의 숫자를 이진수와 십진수로 변환하는 방법은 무엇인가요?
지금까지, 우리는 이진법과 십진법 사이에서 정수를 변환하는 방법을 배웠습니다. 소수 자리가 있는 숫자는 어떻게 할까요? 절차는 위의 단계와 비슷합니다. 먼저, 소수 자리 앞 뒤로 숫자를 나눕니다. 소수를 포함한 1932.1875라는 십진수를 생각해 보겠습니다:
정수부는 1932이고 분수는 0.1875입니다. 1932의 정수부에 대해서는 위의 단계를 사용하세요. 결과로 나오는 이진수는 11110001100입니다.
0.1875의 분수 부분은 다음 스키마에 따라 변환할 수 있습니다. 분수 부분을 재귀적으로 두 배로 곱합니다. 결과가 1을 초과하면 1을 기록하고 결과 숫자에서 1을 뺍니다. 결과가 1보다 작으면 0을 기록합니다. 그렇지 않으면 0을 기록합니다.
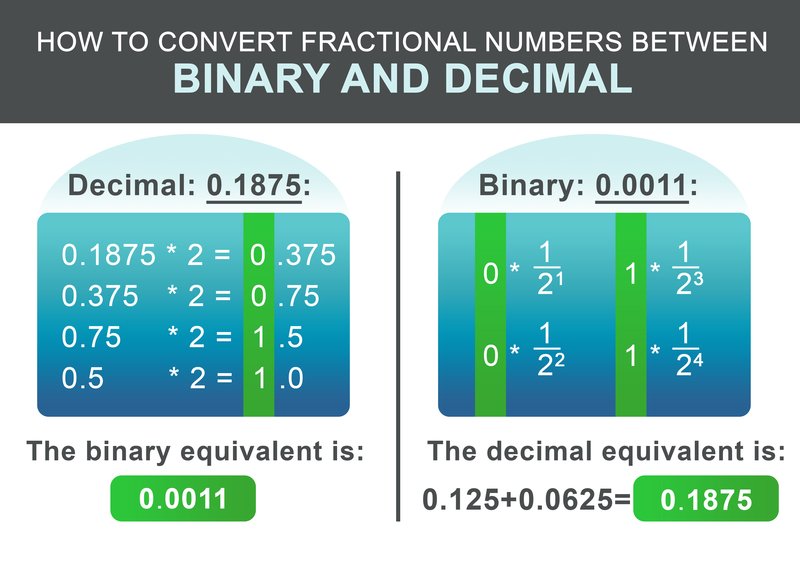
우리의 예시 0.1875에 대한 이진수는 다음과 같습니다: 0.0011 마지막 단계에서 정수 부분과 소수 부분을 더하세요:
$$11110001100.0011$$
이진 소수를 다시 변환하기 위해서는 워크플로우가 훨씬 간단합니다. 소수점 이후 각 자릿수마다 $1/2^i$를 결과에 더하면 됩니다. 여기서 i는 왼쪽에서부터 시작하여 오른쪽에서 자릿수의 위치를 뜻하며 1부터 시작합니다.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
이진수 체계 및 그 응용
숫자 체계는 각 기호가 특정한 가중치를 가지는 서로 다른 조합의 기호들의 세트입니다. 숫자 체계의 주요 특징은 특정한 숫자 체계에서 사용되는 기호의 총 수를 정의하는 진수 또는 기저입니다. 예를 들어, 이진수 체계의 진수는 2이며, 십진수 체계의 진수는 10입니다.
이진법의 자릿수
이진 시스템에서, 우리는 두 가지 다른 숫자를 가지고 있습니다: 0과 1. 컴퓨터에서는 플립플롭 같은 장치를 갖고 있는데, 제어 신호에 따라 두 개의 레벨 중 하나를 저장할 수 있습니다. 더 높은 레벨은 값 1로 할당되고, 더 낮은 레벨은 값 0으로 할당되어 이진 시스템을 형성합니다.
컴퓨팅에서 이진법의 중요성:
컴퓨터는 수십억 개의 트랜지스터를 사용하여 디지털적으로 작동합니다. 디지털이란 이산적인 논리 레벨과 관련이 있습니다. 논리 레벨은 5V, 0V, 10V 등과 같은 다양한 전위 레벨을 의미합니다.
컴퓨터는 모두 이진 논리를 사용하여 작동하기 때문에 우리가 컴퓨터를 나타내려면 진수가 2와 같은 숫자로 작성해야 합니다. 이 숫자 체계의 두 기호는 두 이산 논리 수준과 유사합니다. 편의상, 이 두 기호를 0과 1로 간주하지만 컴퓨터에 있어서 0과 1은 서로 다른 전압 수준을 의미합니다. 일반적으로 0은 낮은 전압 수준으로 간주되고 1은 높은 전압 수준으로 간주됩니다.
모니터 화면이나 마우스 또는 키보드로 입력된 모든 것은 모두 0과 1로 이루어져 있습니다. 유일한 차이점은 그들의 연속적인 배열입니다. 따라서 컴퓨터를 통해 작업을 완료하려면 이진수의 작동 방식과 10진수와의 관계를 알아야 합니다. 왜냐하면 우리가 알고 있는 도메인으로 이진수 영역의 값을 변환해야 하기 때문입니다.
