محول الثنائي إلى عشري: يقوم بتحويل الأعداد الثنائية إلى عشرية والعكس.

---

كيفية تحويل الأرقام الثنائية إلى عشرية:

• الخطوة 1: قم بكتابة الوزن المرتبط بكل رقم في الرقم الثنائي. الوزن هو 2 مرفوع لأس الرقم في الموضع في القراءة من اليمين إلى اليسار.
• الخطوة 2: قم الآن بتسجيل الوزن الذي يكون قيمة الثنائي مساوية للواحد.
• الخطوة 3: أضف جميع الأرقام التي تم الحصول عليها في الخطوة السابقة
• 4: سيكون العدد من الخطوة السابقة هو المكافئ العشري للعدد الثنائي.

لنأخذ في الاعتبار قيمة ثنائية 1101001.

الخطوة الأولى:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{ثنائي} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{الوزن المرتبط} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) الخطوة الثانية: الأوزان التي تكون الأرقام الثنائية 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) الخطوة الثالثة: إضافة جميع الأوزان

$$105 = 64 + 32 + 8 + 1$$

4.) الخطوة الأخيرة: القيمة العشرية المعادلة للثنائية هي:: 105

كيفية تحويل الأعداد العشرية إلى ثنائية:

باتباع هذه الخطوات يمكنك تحويل أي عدد عشري إلى النظام الثنائي:

• الخطوة 1: قسم العدد العشري على 2 واكتب الباقي وامنحه القيمة R1 = الباقي، وبالمثل امنح القيمة Q1 = الناتج المحصل في هذا القسمة.
• الخطوة 2: الآن قسّم Q1 على 2 ولاحظ الباقي. اعط قيمة الباقي لـ R2 وقيمة النتيجة لـ Q1.
• الخطوة 3: استمر في التسلسل حتى تتلقى في وقت ما في القسمة قيمة الناتج (Qn) تساوي صفر.
• الخطوة ٤: يمكنك كتابة الرقم الثنائي على النحو التالي: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

لنأخذ في الاعتبار العدد العشري 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} الآن يمكنك كتابة الرقم الثنائي من البقايا ، بدءًا من R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) عشري = (10110011) ثنائي

كيف يمكن تحويل الأرقام بعد الفاصلة بين النظام العشري ونظام الأعداد الثنائية؟

حتى الآن، تعلمنا كيفية تحويل الأعداد الصحيحة بين النظام الثنائي والعشري. ماذا عن الأعداد التي تحتوي على أماكن عشرية؟ إجراء العملية مشابه للخطوات السابقة. أولاً، قسم العدد إلى جزئيه قبل وبعد الفاصلة العشرية. دعنا نأخذ على سبيل المثال، العدد العشري 1932.1875.

يتكون من جزء عددي 1932 والكسر 0.1875. بالنسبة للجزء العددي 1932 ، استخدم الخطوات المذكورة أعلاه. الناتج الثنائي المكافئ هو: 11110001100.

الجزء الكسري 0.1875 يمكن تحويله وفقًا للمخطط التالي. قم بضرب الجزء الكسري بالعدد 2 تكراريًا. إذا تجاوزت النتيجة الواحد، اكتب 1 ومن ثم اطرح 1 من الرقم الناتج. إذا كانت النتيجة أقل من الواحد، اكتب 0. بعد ذلك، استمر في ضرب الرقم بالعدد 2. وإلا، اكتب 0.

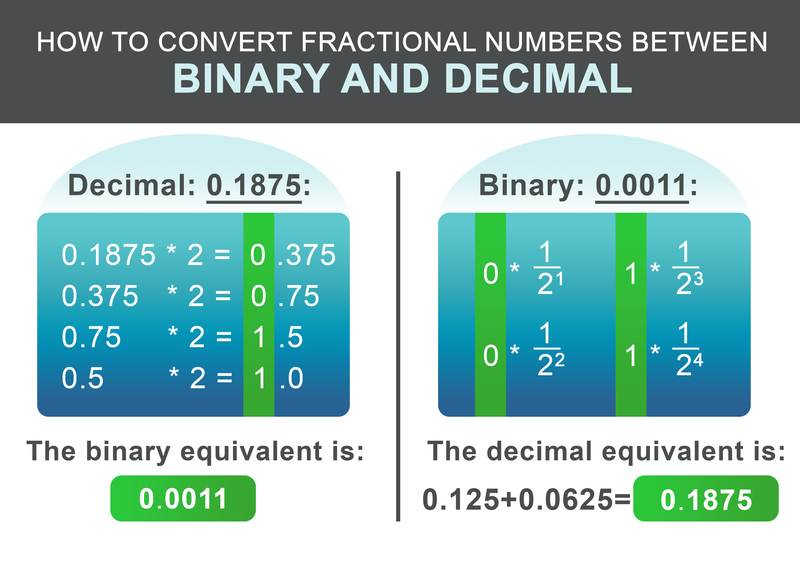
لمثالنا 0.1875 ، فإن الرقم الثنائي الناتج هو: 0.0011 في الخطوة الأخيرة ، قم بإضافة الأجزاء الصحيحة والكسرية:

$$11110001100.0011$$

لتحويل الكسر الثنائي إلى العدد العشري، العملية أبسط بكثير. أضف 1/2^i لكل رقم بعد النقطة إلى النتيجة، حيث يكون i هو موضع الرقم بعد النقطة من اليسار إلى اليمين، بدءًا من 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

نظام الأعداد الثنائي وتطبيقاته

نظام الأعداد هو مجموعة من التركيبات المختلفة للرموز، حيث يحمل كل رمز وزنًا محددًا. والسمات الرئيسية لنظام الأعداد هي القاعدة أو الأساس الذي يحدد إجمالي عدد الرموز المستخدمة في نظام الأعداد المعين. على سبيل المثال، فإن قاعدة نظام الأعداد الثنائي هي 2، وقاعدة نظام الأعداد العشري هي 10.

الفضاء الرقمي للنظام الثنائي

في النظام الثنائي، لدينا رقمين متميزين: 0 و 1. في الحواسيب، لدينا أجهزة مثل الفليب فلوبس التي يمكنها تخزين أي من المستويين وفقًا لإشارة التحكم. يتم تعيين المستوى الأعلى القيمة 1 ويتم تعيين المستوى الأقل القيمة 0، وبالتالي يتشكل النظام الثنائي.

أهمية النظام الثنائي في الحوسبة:

يستخدم الكمبيوتر مليارات من الترانزيستورات التي تعمل بشكل رقمي. مصطلح الرقمي يتعلق بمستويات المنطق الم diskrete. مستويات المنطق هي مختلف مستويات الجهد مثل 5 فولت ، 0 فولت ، 10 فولت ، وغيرها الكثير.

أي كمبيوتر يعمل باستخدام منطق ثنائي ، لذلك إذا أردنا تمثيل الكمبيوتر ، يجب علينا كتابة الأرقام بالقاعدة العشرية المتساوية 2. الرموز الاثنين في هذا النظام العددي تشبه المستويات المنطقية الثنائية المُتمايزة. لسهولتنا ، نعتبر هاتين الرمزين كـ 0 و 1 ، ولكن بالنسبة للكمبيوتر ، فإن الصفر والواحد هما مستويات جهد مختلفة. عمومًا ، يُعتبر الصفر لمستوى الجهد الأقل ويُعتبر الواحد لمستوى الجهد الأعلى.

كل ما نراه على شاشة الكمبيوتر أو ندخله عبر الماوس أو لوحة المفاتيح هو أصفار وواحدات فقط ، الفرق الوحيد هو ترتيبهم التسلسلي. لذا ، إذا كنا نرغب في إنجاز عملنا من الكمبيوتر ، يجب أن نعرف كيف يعمل النظام الثنائي وما هو العلاقة بين النظام الثنائي والعشري لتحويل القيم من المجال الثنائي إلى مجالنا العادي.