
Πώς να μετατρέψετε δυαδικούς αριθμούς σε δεκαδικούς:
- Βήμα 1: Γράψτε το βάρος που σχετίζεται κάτω από κάθε ψηφίο του δυαδικού αριθμού. Το βάρος είναι το 2 επί τη δύναμη της θέσης του ψηφίου στον αριθμό από δεξιά προς τα αριστερά.
- Βήμα 2: Σημειώστε τώρα το βάρος για το οποίο η δυαδική τιμή είναι ίση με 1.
- Βήμα 3: Προσθέστε όλους τους αριθμούς που προέκυψαν στο προηγούμενο βήμα.
- Βήμα 4: Ο αριθμός από το τελευταίο βήμα θα είναι το δεκαδικό ισοδύναμο του δυαδικού αριθμού.
Ας θεωρήσουμε μια δυαδική τιμή 1101001.
1.) Πρώτο βήμα:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{ΔΙΜΕΡΗΣ} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Βάρος που σχετίζεται} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Δεύτερο βήμα: Βάρη για τα οποία τα δυαδικά ψηφία είναι 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Τρίτο βήμα: Προσθήκη όλων των βαρών
$$105 = 64 + 32 + 8 + 1$$
4.) Τελευταίο βήμα: Το δεκαδικό ισοδύναμο του δυαδικού είναι:: 105
Πώς να μετατρέψετε δεκαδικούς αριθμούς σε δυαδικούς:
Ακολουθώντας αυτά τα βήματα μπορείτε να μετατρέψετε οποιονδήποτε δεκαδικό αριθμό στο δυαδικό σύστημα:
- Βήμα 1: Διαιρέστε τον δεκαδικό αριθμό με το 2 και γράψτε το υπόλοιπο και αναθέστε μια τιμή R1 = υπόλοιπο, αναθέτοντας ομοίως την τιμή Q1 = πηλίκο που προκύπτει από αυτή τη διαίρεση.
- Βήμα 2: Τώρα διαιρέστε το Q1 με το 2 και σημειώστε το υπόλοιπο. Αναθέστε την τιμή του υπολοίπου στο R2 και την τιμή του πηλίκου στο Q1.
- Βήμα 3: Συνεχίστε την ακολουθία έως ότου σε κάποιο σημείο μιας διαίρεσης λάβετε την τιμή του πηλίκου (Qn) ίση με 0.
- Βήμα 4: Μπορείτε να γράψετε τον δυαδικό αριθμό ως εξής: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) ΔΙΜΕΡΗΣ
Πώς μετατρέπετε τα ψηφία μετά το δεκαδικό σημείο μεταξύ του δυαδικού και του δεκαδικού αριθμητικού συστήματος;
Μέχρι στιγμής, μάθαμε πώς να μετατρέπουμε ακέραιους αριθμούς μεταξύ δυαδικού και δεκαδικού συστήματος. Τι γίνεται με τους αριθμούς με δεκαδικά ψηφία; Η διαδικασία είναι παρόμοια με τα παραπάνω βήματα. Πρώτα, χωρίστε τον αριθμό στο τμήμα του πριν και μετά το δεκαδικό μέρος. Ας θεωρήσουμε τον δεκαδικό αριθμό 1932,1875:
Αποτελείται από ένα ακέραιο μέρος 1932 και το κλάσμα 0,1875. Για το ακέραιο μέρος 1932, χρησιμοποιήστε τα παραπάνω βήματα. Το δυαδικό ισοδύναμο που προκύπτει είναι: 11110001100.
Το κλασματικό μέρος 0,1875 μπορεί να μετατραπεί σύμφωνα με το ακόλουθο σχήμα. Πολλαπλασιάστε αναδρομικά το κλασματικό μέρος επί δύο. Εάν το αποτέλεσμα υπερβαίνει το 1, γράψτε το 1 και στη συνέχεια αφαιρέστε το 1 από τον αριθμό που προκύπτει. Εάν το αποτέλεσμα είναι μικρότερο από το 1, γράψτε 0. Στη συνέχεια, συνεχίστε τον πολλαπλασιασμό με το δύο. Διαφορετικά, γράψτε το 0.
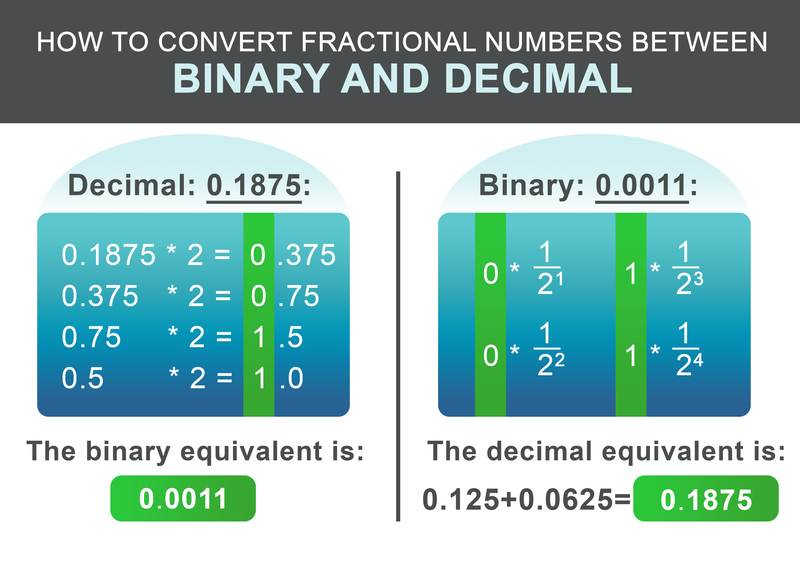
Για το παράδειγμά μας 0,1875, ο δυαδικός αριθμός που προκύπτει είναι: 0,0011 Στο τελευταίο βήμα προσθέστε το ακέραιο και το κλασματικό μέρος:
$$11110001100.0011$$
Για τη μετατροπή της δυαδικής παράταξης πίσω, η ροή εργασίας είναι ακόμη πιο απλή. Προσθέστε $1/2^i$ για κάθε ψηφίο μετά την τελεία στο αποτέλεσμα, όπου i είναι η θέση του ψηφίου μετά από αριστερά προς τα δεξιά, ξεκινώντας από το 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Το δυαδικό σύστημα αριθμών και οι εφαρμογές του
Ένα αριθμητικό σύστημα είναι ένα σύνολο διαφορετικών συνδυασμών συμβόλων, με κάθε σύμβολο να έχει ένα συγκεκριμένο βάρος. Τα κύρια χαρακτηριστικά ενός αριθμητικού συστήματος είναι η ρίζα ή η βάση που καθορίζει τον συνολικό αριθμό των συμβόλων που χρησιμοποιούνται σε ένα συγκεκριμένο αριθμητικό σύστημα. Για παράδειγμα, το radix του δυαδικού συστήματος αριθμών είναι 2 και το radix του δεκαδικού συστήματος αριθμών είναι 10.
Ο ψηφιακός χώρος του δυαδικού συστήματος
Στο δυαδικό σύστημα, έχουμε δύο διαφορετικά ψηφία: Στους υπολογιστές, έχουμε συσκευές όπως τα flip-flops που μπορούν να αποθηκεύσουν οποιοδήποτε από τα δύο επίπεδα σύμφωνα με ένα σήμα ελέγχου. Στο υψηλότερο επίπεδο αποδίδεται η τιμή 1 και στο χαμηλότερο επίπεδο αποδίδεται η τιμή 0, σχηματίζοντας έτσι ένα δυαδικό σύστημα.
Η σημασία του δυαδικού συστήματος στην πληροφορική:
Ένας υπολογιστής χρησιμοποιεί δισεκατομμύρια και δισεκατομμύρια τρανζίστορ που λειτουργούν ψηφιακά. Ο όρος ψηφιακός αφορά τα διακριτά λογικά επίπεδα. Τα λογικά επίπεδα είναι τα διάφορα επίπεδα δυναμικού όπως 5V, 0V, 10v και πολλά άλλα.
Κάθε υπολογιστής λειτουργεί με δυαδική λογική, οπότε αν θέλουμε να αναπαραστήσουμε τον υπολογιστή, πρέπει να γράψουμε τους αριθμούς με radix ίσο με 2. Τα δύο σύμβολα σε αυτό το σύστημα αριθμών είναι ανάλογα με τα δύο διακριτά λογικά επίπεδα. Για την ευκολία μας, θεωρούμε αυτά τα δύο σύμβολα ως 0 και 1, αλλά για έναν υπολογιστή το 0 και το 1 είναι διαφορετικά επίπεδα τάσης. Γενικά, το 0 θεωρείται το χαμηλότερο επίπεδο τάσης και το 1 το υψηλότερο επίπεδο τάσης.
Όλα όσα βλέπουμε στην οθόνη του υπολογιστή ή παρέχουμε την είσοδο μέσω ενός ποντικιού ή πληκτρολογίου είναι όλα 0 και 1, η μόνη διαφορά είναι η διαδοχική τους διάταξη. Έτσι, αν θέλουμε να κάνουμε τη δουλειά μας από τον υπολογιστή πρέπει να γνωρίζουμε πώς λειτουργεί το δυαδικό σύστημα και ποια είναι η σχέση του δυαδικού συστήματος με τους δεκαδικούς αριθμούς για να μετατρέψουμε τις τιμές από το δυαδικό πεδίο στο γνωστό μας πεδίο.
