Enter Decimal OR Binary Number:
Result:
converting binary to decimal

How to convert Binary Numbers to Decimal:

  • Step 1: Write down the weight associated below every digit of the binary number. The weight is 2 by the power of the position of the digit in the number reading from right to left.
  • Step 2: Now note the weight for which the binary value is equal to 1.
  • Step 3: Add all the numbers obtained in the previous step
  • Step 4: The number from the last step will be the decimal equivalent of the binary number.

Let us consider a binary value 1101001.

1.) First step:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY } & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Weight associated } & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Second step: Weights for which binary digits are 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Third step: Adding all the weights

$$105 = 64 + 32 + 8 + 1$$

4.) Last step: The Decimal equivalent of the Binary is: : 105

How to convert Decimal Numbers to Binary:

Following these steps you can convert any decimal number into the binary system:

  • Step 1: Divide the decimal number by 2 and write down the remainder and assign a value R1 = remainder, similarly assigning the value Q1 = quotient obtained in this division.
  • Step 2: Now divide Q1 with 2 and note the remainder. Assign the value of the remainder to R2 and the value of the quotient to Q1.
  • Step 3: Continue the sequence till at some point in a division you get the value of quotient (Qn) equal to 0.
  • Step 4: You can write the binary number as: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
Example: Let us consider the decimal number 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Now you can write down the binary number from the remainders, starting with R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINARY

How do you convert digits after the decimal point between the binary and decimal numeral system?

So far, we have learned how to convert integer numbers between binary and decimal. How about numbers with decimal places? The procedure is similar to the steps above. First, split the number into its part before and after the decimal place. Let's consider the decimal number 1932.1875:

It consists of an integer part 1932 and the fraction 0.1875. For the integer part 1932, use the steps from above. The resulting binary equivalent is: 11110001100.

The fractional part 0.1875 can be converted according to the following schema. Recursively multiply the factional part by two. If the result exceeds 1, write down 1 and then subtract 1 from the resulting number. If the result is less than one write down 0. Next, continue multiplying by two. Otherwise, write down 0.

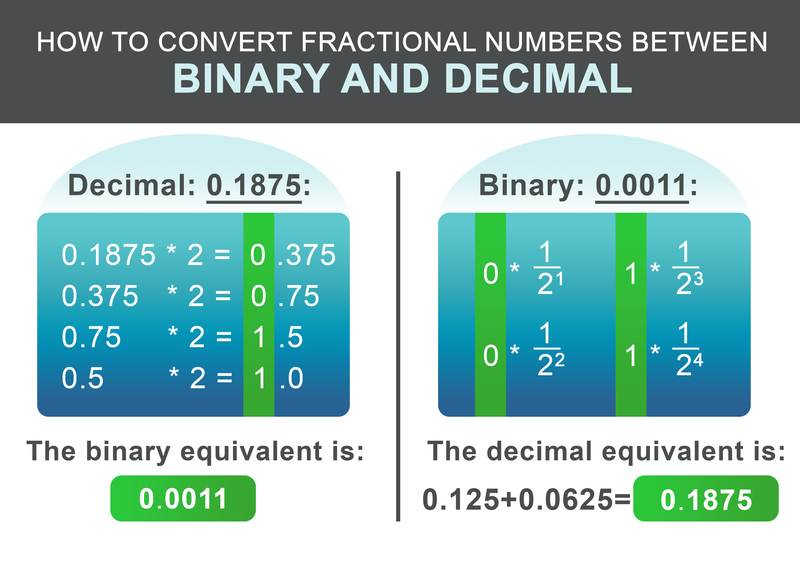
converting binary to decimal

For our example 0.1875, the resulting binary number is: 0.0011 In the last step add the integer and fractional parts:

$$11110001100.0011$$

For converting the binary faction back, the workflow is even simpler. Add $1/2^i$ for each digit after the dot to the result, whereby i is the position of the digit after from the left to the right, starting at 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

The Binary Number System and its Applications

A number system is a set of different combinations of symbols, with each symbol having a specific weight. The main characteristics of a number system are the radix or base that defines the total number of symbols used in a particular number system. For example, the radix of the binary number system is 2, and the radix of the decimal number system is 10.

The Digit Space of the Binary System

In the binary system, we have two distinct digits: 0 and 1. In computers, we have devices like flip-flops which can store any of the two levels according to a control signal. The higher level is assigned the value 1 and the lower level is assigned the value 0, hence forming a binary system.

Importance of the Binary System in Computing:

A computer makes use of billions and billions of transistors that operate digitally. The term digital is concerned with the discrete logic levels. Logic levels are the different potential levels like 5V, 0V, 10v, and many others.

Any computer operates using a binary logic, so if we want to represent the computer, we must write the numbers with radix equal to 2. The two symbols in this number system are analogous to the two discrete logic levels. For our ease, we consider these two symbols as 0 and 1, but for a computer 0 and 1 are different voltage levels. Generally, 0 is considered for the lower voltage level and 1 is considered for the higher voltage level.

All we see on the screen of the computer or provide the input through a mouse or keyboard are all 0s and 1s, the only difference is their sequential arrangement. So, if we want to get our work done from the computer we must know how binary works and what is the relation of binary with decimals to convert the values from the binary domain into our known domain.