
Come convertire i numeri binari in decimali:
- Fase 1: Scrivere il peso associato sotto ogni cifra del numero binario. Il peso è pari a 2 per la potenza della posizione della cifra nel numero, leggendo da destra a sinistra.
- Fase 2: Ora si nota il peso per il quale il valore binario è uguale a 1.
- Fase 3: sommare tutti i numeri ottenuti nella fase precedente
- Fase 4: il numero ottenuto nell'ultima fase sarà l'equivalente decimale del numero binario.
Consideriamo il valore binario 1101001.
1.) Primo passo:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARIO} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Peso associato} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Seconda fase: Pesi per i quali le cifre binarie sono 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Terzo passo: Aggiunta di tutti i pesi
$$105 = 64 + 32 + 8 + 1$$
4.) Ultimo passo: L'equivalente decimale del binario è:: 105
Come convertire i numeri decimali in binari:
Seguendo questi passaggi è possibile convertire qualsiasi numero decimale nel sistema binario:
- Fase 1: Dividere il numero decimale per 2, scrivere il resto e assegnare il valore R1 = resto, assegnando analogamente il valore Q1 = quoziente ottenuto in questa divisione.
- Fase 2: dividere ora Q1 con 2 e annotare il resto. Assegnate il valore del resto a R2 e il valore del quoziente a Q1.
- Fase 3: Continuare la sequenza finché a un certo punto di una divisione non si ottiene il valore del quoziente (Qn) uguale a 0.
- Fase 4: Il numero binario può essere scritto come: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMALE = (10110011) BINARIO
Come si convertono le cifre dopo la virgola tra il sistema numerico binario e quello decimale?
Finora abbiamo imparato a convertire i numeri interi tra binari e decimali. E i numeri con cifre decimali? La procedura è simile a quella descritta sopra. Innanzitutto, si divide il numero nella sua parte prima e dopo la cifra decimale. Consideriamo il numero decimale 1932,1875:
È composto da una parte intera 1932 e dalla frazione 0,1875. Per la parte intera 1932, utilizzare i passaggi precedenti. L'equivalente binario risultante è: 11110001100.
La parte frazionaria 0,1875 può essere convertita secondo il seguente schema. Moltiplicare ricorsivamente la parte frazionaria per due. Se il risultato è superiore a 1, scrivere 1 e poi sottrarre 1 dal numero risultante. Se il risultato è inferiore a 1, scrivere 0. Continuare quindi a moltiplicare per due. Altrimenti, scrivere 0.
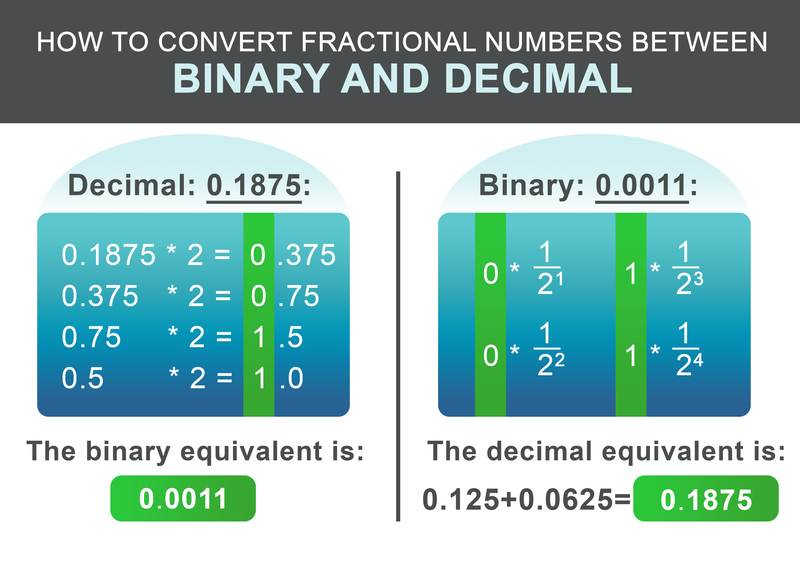
Per il nostro esempio 0,1875, il numero binario risultante è: 0,0011 Nell'ultimo passaggio si sommano le parti intere e frazionarie:
$$11110001100.0011$$
Per la conversione della fazione binaria, il flusso di lavoro è ancora più semplice. Aggiungere $1/2^i$ per ogni cifra dopo il punto al risultato, dove i è la posizione della cifra dopo, da sinistra a destra, a partire da 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
Il sistema numerico binario e le sue applicazioni
Un sistema numerico è un insieme di diverse combinazioni di simboli, con ogni simbolo che ha un peso specifico. Le caratteristiche principali di un sistema numerico sono il radix o la base che definisce il numero totale di simboli utilizzati in un particolare sistema numerico. Ad esempio, il radix del sistema numerico binario è 2, mentre il radix del sistema numerico decimale è 10.
Lo spazio delle cifre del sistema binario
Nel sistema binario abbiamo due cifre distinte: 0 e 1. Nei computer, abbiamo dispositivi come i flip-flop che possono memorizzare uno qualsiasi dei due livelli in base a un segnale di controllo. Al livello più alto viene assegnato il valore 1 e a quello più basso il valore 0, formando così un sistema binario.
Importanza del sistema binario nell'informatica:
Un computer utilizza miliardi e miliardi di transistor che operano in modo digitale. Il termine digitale si riferisce ai livelli logici discreti. I livelli logici sono i diversi livelli di potenziale come 5V, 0V, 10v e molti altri.
Qualsiasi computer funziona con una logica binaria, quindi se vogliamo rappresentare il computer, dobbiamo scrivere i numeri con radix uguale a 2. I due simboli di questo sistema numerico sono analoghi ai due livelli logici discreti. Per comodità, consideriamo questi due simboli come 0 e 1, ma per un computer 0 e 1 sono livelli di tensione diversi. In generale, si considera 0 il livello di tensione più basso e 1 quello più alto.
Tutto ciò che vediamo sullo schermo del computer o che forniamo come input attraverso il mouse o la tastiera sono tutti 0 e 1, l'unica differenza è la loro disposizione sequenziale. Perciò, se vogliamo lavorare al computer, dobbiamo sapere come funziona il binario e qual è la relazione tra binario e decimale per convertire i valori dal dominio binario al nostro dominio noto.
