Pretvornik iz binarnega v decimalni sistem: Pretvarja binarni v decimalni sistem in obratno.

---

Kako pretvoriti binarne številke v decimalne:

• Korak 1: Zapišite težo, povezano z vsako številko binarnega števila. Utež je 2 z močjo položaja številke v številu, ki se bere od desne proti levi.
• Korak 2: Zdaj zapišite utež, za katero je binarna vrednost enaka 1.
• Korak 3: Seštejte vsa števila, dobljena v prejšnjem koraku
• Korak 4: Številka iz zadnjega koraka bo decimalni ekvivalent binarnega števila.

Obravnavajmo binarno vrednost 1101001.

1.) Prvi korak:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARNI} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Povezana teža} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Drugi korak: Uteži, za katere so binarne številke enake 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Tretji korak: Seštevanje vseh uteži

$$105 = 64 + 32 + 8 + 1$$

4.) Zadnji korak: Decimalni ekvivalent binarnega zapisa je:: 105

Kako pretvoriti decimalna števila v binarno:

Po teh korakih lahko katero koli decimalno število pretvorite v binarni sistem:

• Korak 1: decimalno število delimo z 2, zapišemo ostanek in mu pripišemo vrednost R1 = ostanek, podobno pripišemo vrednost Q1 = kvocient, ki ga dobimo pri deljenju.
• Korak 2: Zdaj delite Q1 z 2 in zapišite preostanek. Vrednost ostanka pripišite R2, vrednost kvocienta pa Q1.
• Korak 3: Nadaljujte z zaporedjem, dokler na neki točki deljenja ne dobite vrednosti kvocienta (Qn), ki je enaka 0.
• 4. korak: Binarno število lahko zapišete kot: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Primer: Vzemimo decimalno število 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Zdaj lahko zapišete binarno število iz ostankov, začenši z R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMALNO = (10110011) BINARNI

Kako pretvoriti števke za decimalno vejico med dvojiškim in desetiškim številskim sistemom?

Do zdaj smo se naučili, kako pretvoriti cela števila med dvojiškim in desetiškim sistemom. Kaj pa števila z decimalnimi mesti? Postopek je podoben zgornjim korakom. Najprej razdelimo število na del pred in za decimalnim mestom. Poglejmo decimalno število 1932,1875:

Sestavljen je iz celega števila 1932 in ulomka 0,1875. Za celoštevilski del 1932 uporabite zgornje korake. Dobljeni binarni ekvivalent je: 11110001100.

Delni del 0,1875 se lahko pretvori v skladu z naslednjo shemo. Rekurzivno pomnožite frakcijski del z dva. Če je rezultat večji od 1, zapišemo 1 in nato od dobljenega števila odštejemo 1. Če je rezultat manjši od 1, zapišemo 0. Nato nadaljujemo z množenjem z dva. V nasprotnem primeru zapišite 0.

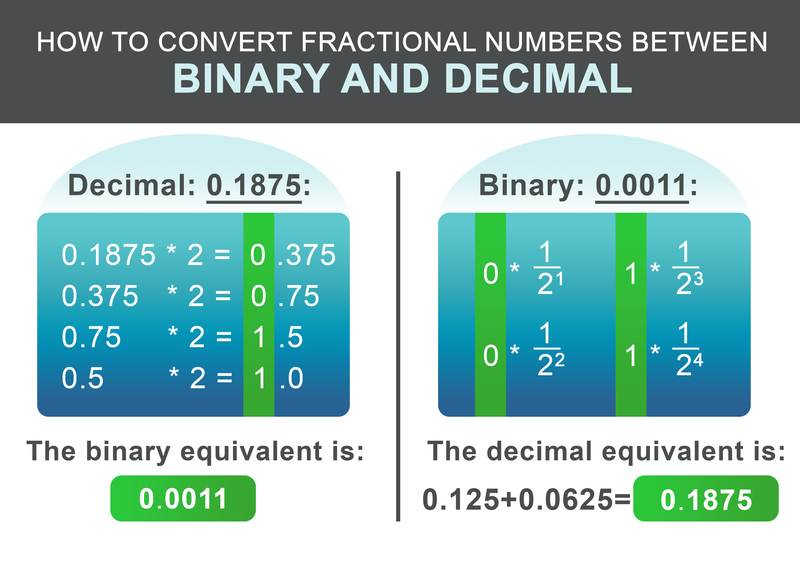
Za naš primer 0,1875 je binarno število: 0,0011 V zadnjem koraku seštejemo celoštevilski in ulomni del:

$$11110001100.0011$$

Za pretvorbo binarne frakcije nazaj je delovni postopek še preprostejši. Rezultatu dodajte $1/2^i$ za vsako števko za piko, pri čemer je i položaj števke za piko od leve proti desni, začenši pri 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Binarni številski sistem in njegove aplikacije

Številski sistem je niz različnih kombinacij simbolov, pri čemer ima vsak simbol določeno težo. Glavne značilnosti številskega sistema so radix ali osnova, ki določa skupno število simbolov, uporabljenih v določenem številskem sistemu. Na primer, radix dvojiškega številskega sistema je 2, radix desetiškega številskega sistema pa je 10.

Prostor številk binarnega sistema

V binarnem sistemu imamo dve različni številki: V računalnikih imamo naprave, kot so flip-flopi, ki lahko shranijo katero koli od dveh ravni v skladu s krmilnim signalom. Višji ravni je dodeljena vrednost 1, nižji ravni pa vrednost 0, s čimer se oblikuje binarni sistem.

Pomen dvojiškega sistema v računalništvu:

Računalnik uporablja milijarde in milijarde tranzistorjev, ki delujejo digitalno. Izraz digitalni se nanaša na diskretne logične ravni. Logični nivoji so različni potencialni nivoji, kot so 5 V, 0 V, 10 V in številni drugi.

Vsak računalnik deluje z binarno logiko, zato moramo, če želimo predstaviti računalnik, zapisati števila z radixom, ki je enak 2. Dva simbola v tem številskem sistemu sta analogna dvema diskretnima logičnima nivojema. Za lažjo predstavo ta dva simbola obravnavamo kot 0 in 1, vendar sta za računalnik 0 in 1 različni ravni napetosti. Na splošno velja, da je 0 nižja raven napetosti, 1 pa višja raven napetosti.

Vse, kar vidimo na zaslonu računalnika ali vnesemo z miško ali tipkovnico, so vse 0 in 1, razlika je le v njihovi zaporedni razporeditvi. Če torej želimo opraviti delo z računalnikom, moramo vedeti, kako deluje binarni sistem in kakšno je razmerje med njim in decimalkami, da lahko pretvorimo vrednosti iz binarnega področja v nam znano področje.