Prevodník z binárnej do desiatkovej sústavy: Prevádza binárnu do desiatkovej sústavy a naopak.

---

Ako previesť binárne čísla na desiatkové:

• Krok 1: Zapíšte váhu priradenú pod každú číslicu binárneho čísla. Váha je 2 na mocninu pozície číslice v čísle čítanej sprava doľava.
• Krok 2: Teraz si všimnite váhu, pre ktorú je binárna hodnota rovná 1.
• Krok 3: Súčet všetkých čísel získaných v predchádzajúcom kroku
• Krok 4: Číslo z posledného kroku bude desiatkovým ekvivalentom binárneho čísla.

Uvažujme binárnu hodnotu 1101001.

1.) Prvý krok:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINÁRNE} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Hmotnosť súvisiaca s} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Druhý krok: Váhy, pre ktoré sú binárne číslice 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3.) Tretí krok: Sčítanie všetkých váh

$$105 = 64 + 32 + 8 + 1$$

4.) Posledný krok: Desiatkový ekvivalent binárneho súboru je:: 105

Ako previesť desiatkové čísla do dvojkovej sústavy:

Podľa týchto krokov môžete previesť akékoľvek desiatkové číslo do dvojkovej sústavy:

• Krok 1: Desatinné číslo vydeľte dvomi, zapíšte zvyšok a priraďte hodnotu R1 = zvyšok, podobne priraďte hodnotu Q1 = kvocient získaný pri tomto delení.
• Krok 2: Teraz vydeľte Q1 číslom 2 a zapíšte si zvyšok. Hodnotu zvyšku priraďte k R2 a hodnotu kvocientu k Q1.
• Krok 3: Pokračujte v postupnosti, kým v niektorom bode delenia nedostanete hodnotu kvocientu (Qn) rovnú 0.
• Krok 4: Binárne číslo môžete zapísať ako: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Príklad: Uvažujme desatinné číslo 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Teraz môžete zapísať binárne číslo zo zvyškov, počnúc R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) DECIMAL = (10110011) BINÁRNE

Ako previesť číslice za desatinnou bodkou medzi dvojkovou a desiatkovou číselnou sústavou?

Doteraz sme sa učili, ako previesť celé čísla medzi binárnym a desiatkovým systémom. A čo čísla s desatinnými miestami? Postup je podobný vyššie uvedeným krokom. Najprv rozdeľte číslo na jeho časť pred a za desatinným miestom. Uvažujme desatinné číslo 1932,1875:

Skladá sa z celočíselnej časti 1932 a zlomku 0,1875. Pre celočíselnú časť 1932 použite postup uvedený vyššie. Výsledný binárny ekvivalent je: 11110001100.

Zlomkovú časť 0,1875 možno previesť podľa nasledujúcej schémy. Rekurzívne vynásobte zlomkovú časť dvoma. Ak je výsledok väčší ako 1, zapíš 1 a potom od výsledného čísla odčítaj 1. Ak je výsledok menší ako 1, zapíšte 0. Ďalej pokračujte v násobení dvoma. V opačnom prípade zapíšte 0.

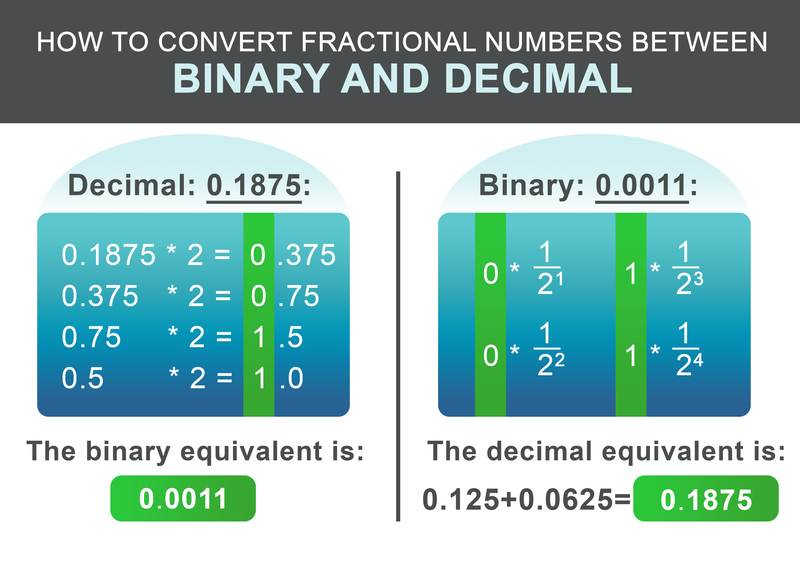
Pre náš príklad 0,1875 je výsledné binárne číslo: 0,0011 V poslednom kroku sa sčítajú celé a zlomkové časti:

$$11110001100.0011$$

Pri konverzii binárnej frakcie späť je pracovný postup ešte jednoduchší. K výsledku pripočítajte $1/2^i$ za každú číslicu po bodke, pričom i je pozícia číslice po zľava doprava, počnúc číslicou 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Binárna číselná sústava a jej aplikácie

Číselný systém je súbor rôznych kombinácií symbolov, pričom každý symbol má určitú váhu. Hlavnými charakteristikami číselnej sústavy sú radix alebo základ, ktorý určuje celkový počet symbolov použitých v konkrétnej číselnej sústave. Napríklad radix binárnej číselnej sústavy je 2 a radix desiatkovej číselnej sústavy je 10.

Číselný priestor dvojkovej sústavy

V binárnej sústave máme dve rôzne číslice: V počítačoch máme zariadenia ako flip-flopy, ktoré môžu ukladať ktorúkoľvek z týchto dvoch úrovní podľa riadiaceho signálu. Vyššej úrovni sa priradí hodnota 1 a nižšej úrovni sa priradí hodnota 0, čím sa vytvorí binárna sústava.

Význam binárnej sústavy vo výpočtovej technike:

Počítač využíva miliardy a miliardy tranzistorov, ktoré pracujú digitálne. Pojem digitálny sa týka diskrétnych logických úrovní. Logické úrovne sú rôzne potenciálne úrovne, ako napríklad 5 V, 0 V, 10 V a mnohé ďalšie.

Každý počítač pracuje pomocou binárnej logiky, takže ak chceme reprezentovať počítač, musíme zapisovať čísla s radixom rovným 2. Dva symboly v tejto číselnej sústave sú analogické dvom diskrétnym logickým úrovniam. Pre naše uľahčenie považujeme tieto dva symboly za 0 a 1, ale pre počítač sú 0 a 1 rôzne úrovne napätia. Vo všeobecnosti sa 0 považuje za nižšiu napäťovú úroveň a 1 za vyššiu napäťovú úroveň.

Všetko, čo vidíme na obrazovke počítača alebo zadávame prostredníctvom myši či klávesnice, sú samé 0 a 1, jediným rozdielom je ich postupné usporiadanie. Ak teda chceme z počítača dostať svoju prácu, musíme vedieť, ako funguje dvojková sústava a aký je vzťah dvojkovej sústavy s desatinnými číslami, aby sme mohli hodnoty z dvojkovej oblasti previesť do nám známej oblasti.