Перетворювач двійкової на десяткову систему числення: Перетворює двійкову на десяткову та навпаки.

---

Як перетворити двійкові числа на десяткові:

• Крок 1: Запишіть вагу, що відповідає кожній цифрі двійкового числа, нижче. Вага дорівнює 2 у степені положення цифри в числі, що читається зправа наліво.
• Крок 2: зараз зауважте масу, для якої двійкове значення дорівнює 1.
• Крок 3: Додайте всі отримані на попередньому кроці числа
• Крок 4: число з попереднього кроку буде десятковим еквівалентом двійкового числа.

Давайте розглянемо двійкове значення 1101001.

1.) Перший крок:

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{ДВІЙКОВИЙ } & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Пов'язана вага } & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}

2.) Другий крок: Ваги, для яких бінарні розряди дорівнюють 1.

\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}

3) Третій крок: додавання всіх ваг

$$105 = 64 + 32 + 8 + 1$$

4.) Останній крок: Десятковий еквівалент двійкового числа: : 105

Як перетворити десяткові числа на двійкові:

Виконавши ці кроки, ви можете перетворити будь-яке десяткове число в двійкову систему:

• Крок 1: Розділіть десяткове число на 2 і запишіть залишок, присвоюючи значення R1 = залишок, а так само присвойте значення Q1 = частка, отримана в цьому діленні.
• Крок 2: зараз поділіть Q1 на 2 і запишіть залишок. Присвойте значення залишку R2, а значення частки - Q1.
• Крок 3: Продовжуйте послідовність до того часу, поки на деякому етапі ділення значення частки (Qn) не буде дорівнювати 0.
• Крок 4: Ви можете записати двійкове число як: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$

Приклад: Розглянемо десяткове число 179. \begin{array}{|c|c|c|c|c|c|c|} \hline \text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\ \hline \text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\ \text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\ \text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\ \text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\ \text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\ \text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\ \text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\ \text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\ \hline \end{array} Зараз можна записати двійкове число з кінцевиків, починаючи з R8: \begin{array}{|c|c|c|c|c|c|c|} \hline \text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\ \hline \text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\ \hline \end{array}

(179) ДЕСЯТИЧНИЙ = (10110011) ДВІЙКОВИЙ

Які цифри після коми в десятковій та двійковій числовій системах можна перетворити?

Досі ми вивчали, як перетворювати цілі числа між двійковою та десятковою системами. А що на рахунок чисел з десятковим розділовим знаком? Процедура схожа на описані вище кроки. По-перше, розбийте число на частину перед і після десяткового розряду. Розглянемо десяткове число 1932,1875:

Воно складається з цілої частини 1932 та дробу 0,1875. Для цілої частини 1932 використовуйте кроки згори. Отриманий двійковий еквівалент: 11110001100.

Частину 0,1875 можна перетворити за такою схемою. Рекурсивно множимо частину меншу за 2. Якщо результат перевищує 1, записуємо 1, а потім від числа віднімаємо 1. Якщо результат менше одиниці, записуємо 0. Далі продовжуємо множити на два. Інакше записуємо 0.

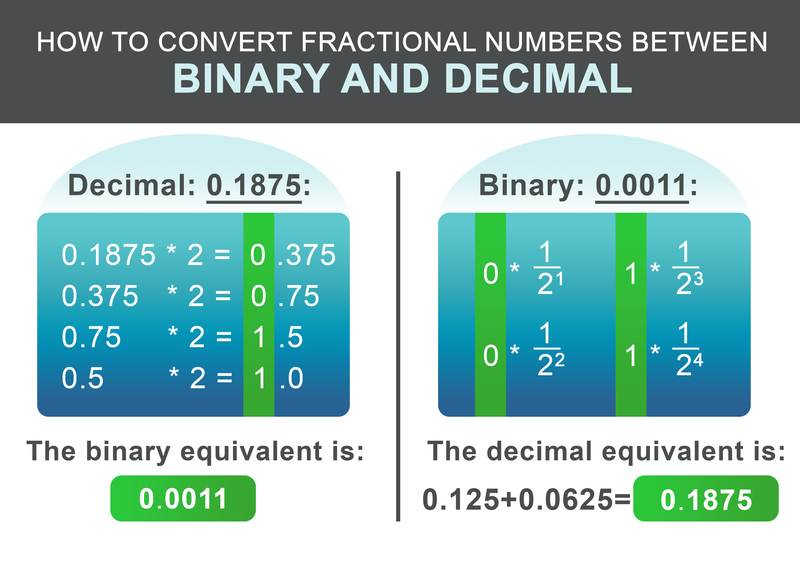
Для нашого прикладу 0,1875 отримане двійкове число: 0.0011 На останньому кроці додайте цілу та дробову частини:

$$11110001100.0011$$

Щоб знову перетворити на двійковий десятковий знак, робота виконується ще простіше. Додайте $1/2^i$ до результату за кожною цифрою після крапки, де i - це положення цифри після крапки зліва направо, починаючи з 1.

$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$

Двійкова числова система і її застосування

Система числення - це набір різних комбінацій символів, причому кожен символ має певну вагу. Основними характеристиками числової системи є основа або база, яка визначає загальну кількість символів, що використовуються в певній числовій системі. Наприклад, основа двійкової числової системи дорівнює 2, а основа десяткової числової системи дорівнює 10.

Цифровий простір двійкової системи

У двійковій системі ми маємо дві відмінні цифри: 0 і 1. У комп'ютерах ми маємо пристрої, такі як тригери, які можуть зберігати будь-який з двох рівнів відповідно до сигналу керування. Вищий рівень має значення 1, а нижчий - значення 0, тим самим утворюючи двійкову систему.

Значення двійкової системи у сфері обчислень:

Комп'ютер використовує мільярди транзисторів, які працюють у цифровому режимі. Термін "цифровий" стосується дискретних рівнів логіки. Рівні логіки - це різні потенційні рівні, такі як 5В, 0В, 10В та багато інших.

Будь-який комп'ютер працює за допомогою двійкової логіки, тому якщо ми хочемо зображувати комп'ютер, ми повинні писати числа з основою, рівною 2. Два символи в цій числовій системі аналогічні двом дискретним рівням логіки. Для нашої зручності ми розглядаємо ці два символи як 0 і 1, але для комп'ютера 0 і 1 - різні рівні напруги. Загалом, 0 вважається меншим рівнем напруги, а 1 - більшим.

Усе, що ми бачимо на екрані комп'ютера або подаємо на вхід за допомогою миші або клавіатури - це самі нулі та одиниці, їх єдина відмінність - це їх послідовний порядок. Таким чином, якщо ми хочемо завершити свою роботу на комп'ютері, ми повинні знати, як працює двійкова система числення і які взаємозв'язки в ній з десятковою системою числення, щоб перетворити значення з двійкової області в нашу відому область.