
Cómo convertir números binarios a decimales:
- Paso 1: Escribe el peso asociado debajo de cada dígito del número binario. El peso es 2 por la potencia de la posición del dígito en el número leyendo de derecha a izquierda.
- Paso 2: Ahora anote el peso para el cual el valor binario es igual a 1.
- Paso 3: Sumar todos los números obtenidos en el paso anterior
- Paso 4: El número del último paso será el equivalente decimal del número binario.
Consideremos un valor binario 1101001.
1.) Primer paso:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARIO} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Peso asociado} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Segundo paso: Pesos para los que los dígitos binarios son 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Tercer paso: Sumar todos los pesos
$$105 = 64 + 32 + 8 + 1$$
4.) Último paso: El equivalente decimal del binario es:: 105
Cómo convertir números decimales a binarios:
Siguiendo estos pasos puedes convertir cualquier número decimal al sistema binario:
- Paso 1: Dividir el número decimal entre 2 y anotar el resto y asignar un valor R1 = resto, asignando igualmente el valor Q1 = cociente obtenido en esta división.
- Paso 2: Ahora divide Q1 entre 2 y anota el resto. Asigna el valor del resto a R2 y el valor del cociente a Q1.
- Paso 3: Continuar la secuencia hasta que en algún momento de una división se obtenga el valor del cociente (Qn) igual a 0.
- Paso 4: Puedes escribir el número binario como $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARIO
¿Cómo se convierten los dígitos después del punto decimal entre el sistema numérico binario y el decimal?
Hasta ahora hemos aprendido a convertir números enteros entre binarios y decimales. ¿Qué pasa con los números con decimales? El procedimiento es similar a los pasos anteriores. En primer lugar, hay que dividir el número en su parte anterior y posterior al decimal. Consideremos el número decimal 1932,1875:
Consta de una parte entera 1932 y la fracción 0,1875. Para la parte entera 1932, utilice los pasos de arriba. El equivalente binario resultante es 11110001100.
La parte fraccionaria 0,1875 se puede convertir según el siguiente esquema. Multiplique recursivamente la parte fraccionaria por dos. Si el resultado es superior a 1, anote 1 y luego reste 1 al número resultante. Si el resultado es inferior a uno, anote 0. A continuación, continúe multiplicando por dos. En caso contrario, anota 0.
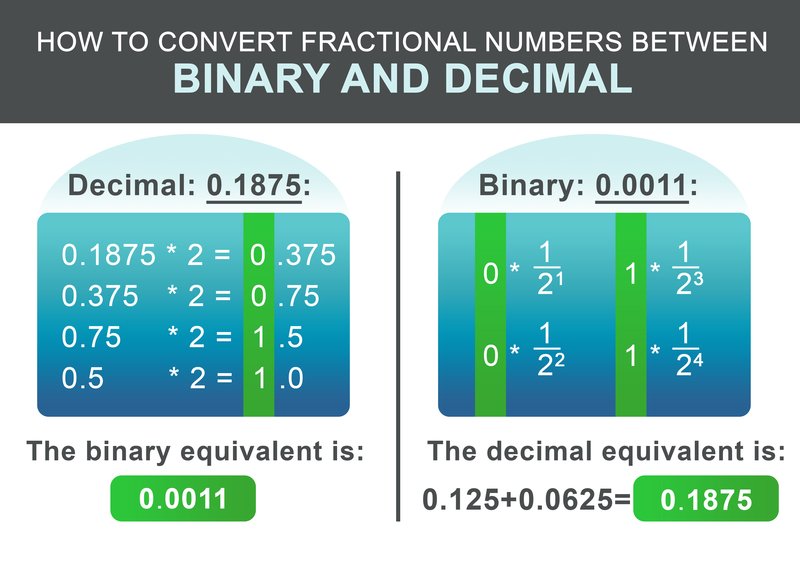
Para nuestro ejemplo 0,1875, el número binario resultante es: 0,0011 En el último paso se suman las partes enteras y fraccionarias:
$$11110001100.0011$$
Para convertir la facción binaria de nuevo, el flujo de trabajo es aún más simple. Añadir $1/2^i$ para cada dígito después del punto al resultado, por lo que i es la posición del dígito después de la izquierda a la derecha, a partir de 1.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
El sistema numérico binario y sus aplicaciones
Un sistema numérico es un conjunto de diferentes combinaciones de símbolos, en el que cada símbolo tiene un peso específico. Las principales características de un sistema numérico son el radix o la base que define el número total de símbolos utilizados en un sistema numérico concreto. Por ejemplo, el radix del sistema numérico binario es 2, y el radix del sistema numérico decimal es 10.
El espacio de los dígitos del sistema binario
En el sistema binario, tenemos dos dígitos distintos: 0 y 1. En los ordenadores, tenemos dispositivos como los flip-flops que pueden almacenar cualquiera de los dos niveles según una señal de control. Al nivel superior se le asigna el valor 1 y al nivel inferior el valor 0, formando así un sistema binario.
Importancia del sistema binario en la informática:
Un ordenador utiliza miles de millones de transistores que funcionan de forma digital. El término digital se refiere a los niveles lógicos discretos. Los niveles lógicos son los diferentes niveles de potencial como 5V, 0V, 10v, y muchos otros.
Cualquier ordenador funciona utilizando una lógica binaria, por lo que si queremos representar el ordenador, debemos escribir los números con radix igual a 2. Los dos símbolos de este sistema numérico son análogos a los dos niveles lógicos discretos. Para nuestra facilidad, consideramos estos dos símbolos como 0 y 1, pero para un ordenador 0 y 1 son niveles de tensión diferentes. Generalmente, el 0 se considera para el nivel de tensión más bajo y el 1 para el nivel de tensión más alto.
Todo lo que vemos en la pantalla del ordenador o proporcionamos la entrada a través de un ratón o teclado son todos 0s y 1s, la única diferencia es su disposición secuencial. Por lo tanto, si queremos realizar nuestro trabajo desde el ordenador debemos saber cómo funciona el binario y cuál es la relación del binario con los decimales para convertir los valores del dominio binario a nuestro dominio conocido.
