
Hogyan lehet a bináris számokat decimálisra konvertálni:
- 1. lépés: Írja fel a bináris szám minden egyes számjegye alá a hozzá tartozó súlyt. A súly a számjegy helyének a számban jobbról balra olvasva a számjegy pozíciójának a 2-es hatványával egyenlő.
- 2. lépés: Most jegyezzük fel azt a súlyt, amelynek bináris értéke 1.
- 3. lépés: Adjuk össze az előző lépésben kapott számokat.
- 4. lépés: Az utolsó lépésben kapott szám lesz a bináris szám decimális megfelelője.
Tekintsük a 1101001 bináris értéket.
1.) Első lépés:
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{BINARY} & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\ \hline \text{Súly társított} & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\ \hline \end{array}2.) Második lépés: Azok a súlyok, amelyeknél a bináris számjegyek 1.
\begin{array}{|c|c|c|c|c|c|c|} \hline \text{64} & \text{32} & \text{8} & \text{1} \\ \hline \end{array}3.) Harmadik lépés: Az összes súly összeadása
$$105 = 64 + 32 + 8 + 1$$
4.) Utolsó lépés: A bináris szám decimális megfelelője a következő:: 105
Hogyan lehet a decimális számokat binárisra konvertálni:
A következő lépésekkel bármilyen decimális számot átkonvertálhat a bináris rendszerbe:
- 1. lépés: Osszuk el a tizedes számot 2-vel, írjuk fel a maradékot, és rendeljük hozzá az R1 = maradék értéket, és hasonlóan rendeljük hozzá a Q1 = az osztás során kapott hányados értékét.
- 2. lépés: Most osszuk el a Q1-et 2-vel, és jegyezzük fel a maradékot. A maradék értékét rendeljük R2-hez, a hányados értékét pedig Q1-hez.
- 3. lépés: Folytassuk a sorozatot addig, amíg egy osztás egy pontján a hányados (Qn) értéke 0 lesz.
- 4. lépés: A bináris számot a következőképpen írhatjuk fel: $$ R(n) R(n-1) . . . . . . . . . . . . . . . . . . . . . R3 R2 R1 $$
(179) DECIMAL = (10110011) BINARY
Hogyan konvertálhatók a tizedespont utáni számjegyek a bináris és a decimális számrendszer között?
Eddig megtanultuk, hogyan lehet egész számokat bináris és decimális számrendszerbe konvertálni. Mi a helyzet a tizedesjegyekkel rendelkező számokkal? Az eljárás hasonló a fenti lépésekhez. Először is osszuk fel a számot a tizedesjegy előtti és utáni részre. Vegyük az 1932,1875 tizedesjegyű számot:
Ez az 1932 egész számból és a 0,1875 törtrészből áll. Az 1932 egész szám részhez a fenti lépéseket alkalmazzuk. Az így kapott bináris egyenérték a következő: 11110001100.
A 0,1875 törtrész a következő séma szerint alakítható át. Szorozzuk meg rekurzívan a törtrészt kettővel. Ha az eredmény meghaladja az 1-et, írjunk le 1-et, majd vonjunk ki 1-et az így kapott számból. Ha az eredmény kisebb, mint 1, írjuk le a 0-t. Ezután folytassuk a kettővel való szorzást. Ellenkező esetben írjuk le a 0-t.
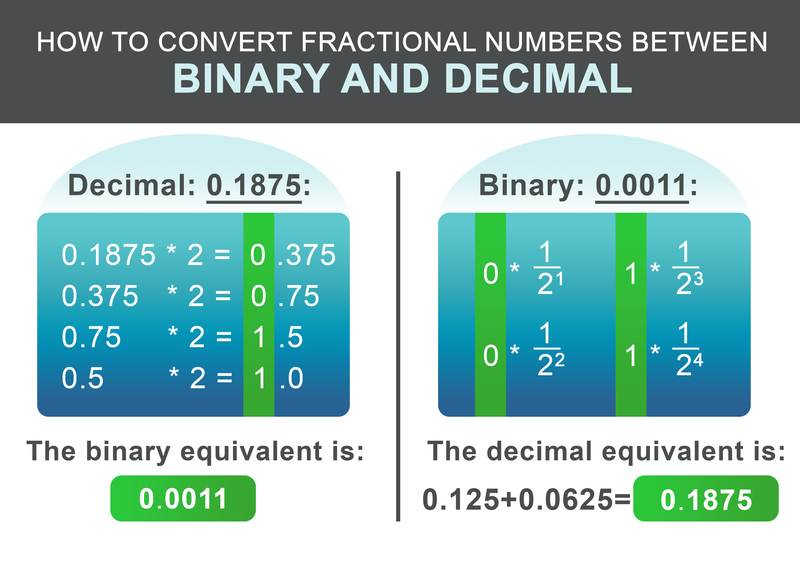
Példánkban 0,1875, az eredményül kapott bináris szám: 0,0011 Az utolsó lépésben adjuk össze az egész és a tört részeket:
$$11110001100.0011$$
A bináris frakció visszaalakításához a munkafolyamat még egyszerűbb. Adjunk hozzá $1/2^i$-t minden egyes pont utáni számjegyhez az eredményhez, ahol i az utána következő számjegy pozíciója balról jobbra, 1-gyel kezdve.
$$ 0 * \frac{1}{2^1} + 0 * \frac{1}{2^2} + 1 * \frac{1}{2^3} + 1 * \frac{1}{2^4} = 0.1875 $$
A bináris számrendszer és alkalmazásai
A számrendszer a szimbólumok különböző kombinációinak halmaza, ahol minden szimbólumnak meghatározott súlya van. A számrendszer fő jellemzői a radix vagy bázis, amely meghatározza az adott számrendszerben használt szimbólumok teljes számát. Például a bináris számrendszer radixa 2, a decimális számrendszer radixa pedig 10.
A bináris rendszer számjegytere
A bináris rendszerben két különböző számjegy van: A számítógépekben olyan eszközökkel rendelkezünk, mint a flip-flopok, amelyek a két szint bármelyikét tárolhatják egy vezérlőjelnek megfelelően. A magasabb szinthez az 1 értéket, az alacsonyabb szinthez pedig a 0 értéket rendeljük, így alakul ki a bináris rendszer.
A bináris rendszer jelentősége a számítástechnikában:
A számítógép több milliárd tranzisztort használ, amelyek digitálisan működnek. A digitális kifejezés a diszkrét logikai szintekre vonatkozik. A logikai szintek a különböző potenciális szintek, mint például 5V, 0V, 10V és sok más.
Minden számítógép bináris logikával működik, így ha a számítógépet akarjuk ábrázolni, akkor a számokat 2-vel egyenlő radixszal kell írnunk. A két szimbólum ebben a számrendszerben analóg a két diszkrét logikai szintnek. A könnyebbség kedvéért ezt a két szimbólumot 0-nak és 1-nek tekintjük, de egy számítógép számára a 0 és az 1 különböző feszültségszinteket jelent. Általában a 0 az alacsonyabb feszültségszintet, az 1 pedig a magasabb feszültségszintet jelenti.
Mindaz, amit a számítógép képernyőjén látunk, vagy amit az egérrel vagy a billentyűzettel adunk meg, mind 0 és 1, az egyetlen különbség a sorrendi elrendezésük. Tehát, ha a számítógép segítségével szeretnénk elvégezni a munkánkat, tudnunk kell, hogyan működik a bináris számrendszer, és mi a bináris számrendszer és a tizedes számok kapcsolata, hogy az értékeket a bináris tartományból az általunk ismert tartományba konvertálhassuk.
