Hvordan konverteres mellem oktale og decimale talsystemer?
Før vi går ind i diskussionen om konvertering af et talsystem til et andet, skal vi tale lidt om selve talsystemet. Talsystemet kan defineres som et sæt af forskellige kombinationer af symboler, hvor hvert symbol har en bestemt vægt. Ethvert talsystem er differentieret på grundlag af radix eller den base, som talsystemet er lavet på. Radix eller basen definerer det samlede antal forskellige symboler, der anvendes i et bestemt talsystem. F.eks. er radix i det binære talsystem 2, radix i det decimale talsystem 10, og radix i det oktale talsystem 8.
Det oktale talsystem:
Som navnet tydeligt antyder, er dette talsystem baseret på radix lig med 8. Så i dette talsystem har vi otte forskellige cifre. For nemheds skyld betragter vi disse otte cifre som de samme som de første otte cifre i det decimale talsystem. Hvert oktalcifres position er forbundet med en potens af 8, og denne potens er lig med indekset for cifferet fra venstre position. Der skal højst tre binære cifre til at repræsentere et oktal tal i binær form. Da basen i dette talsystem selv er en potens af to, er det meget nemt og bekvemt at konvertere oktaltal til binære eller hexadecimale talsystemer, som bruges i computere til at udføre alt arbejde.
Oktal-tallene finder ikke direkte anvendelse i computermaskineriet, fordi computere arbejder med binære tilstande eller bits. Men da oktaltallet har færre cifre til at blive repræsenteret i binære tal, kan det effektivt lagres i computeren uden spild af plads i hukommelsen, ligesom BCD-tallet (binært kodet decimaltal).
Konvertering af decimaltal til oktaltalsystem:
Konvertering af decimaltal til oktal svarer meget til konvertering af decimaltal til binærtal. Den eneste forskel er, at vi denne gang vil dividere det decimale tal med 8 i stedet for 2. Konverteringen kan foretages ved at følge nedenstående trin:
- Trin 1: Divider decimaltallet med 8, noter resten og tildel det værdien R1. På samme måde noteres kvotienten og tildeles værdien Q1.
- Trin2: Divider nu Q1 med 8, noter resten og kvotienten. Tildel værdien R2 og Q2 til den rest og kvotient, der er opnået i dette trin.
- Trin3: Gentag sekvensen, indtil du får værdien af kvotienten (Qn) lig med 0.
- Trin4: Det oktale tal vil se sådan ud: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Eksempel: Lad os tage et decimaltal 2181 i betragtning.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Så OCTAL-ækvivalenten til 2181 er:
(2181) Decimal = (4205) Octal
Konvertering af oktal til binært talsystem:
Igen er konverteringen af oktal til decimaltal meget lig konverteringen af binært til decimaltal, den eneste forskel er, at vi denne gang vil gange cifrene med 8 potenser i stedet for 2. Konverteringen kan udføres ved at følge de nedenfor beskrevne trin:
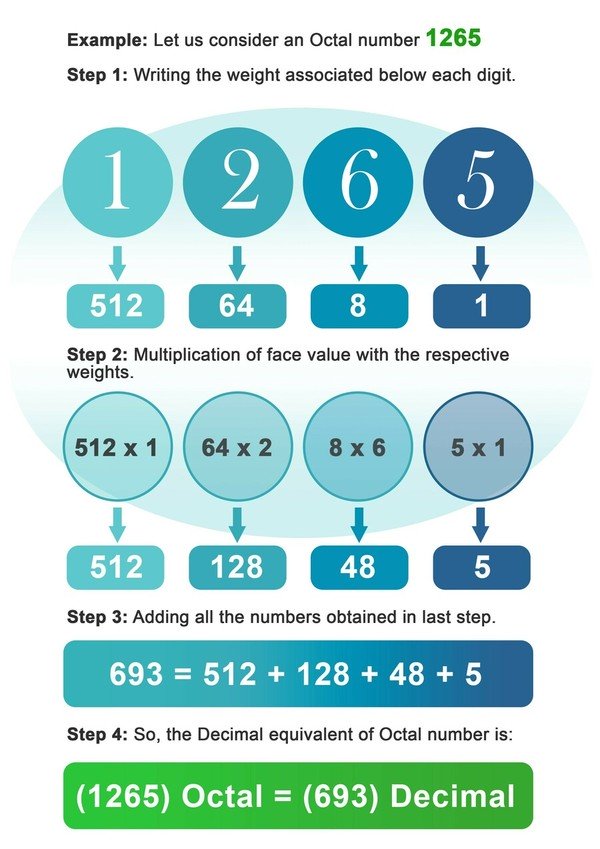
- Trin 1: Skriv vægten af 8 ned under hvert ciffer i oktaltallet.
- Trin 2: Multiplicer nu hvert ciffer med den vægt, der er knyttet til det pågældende sted eller indeks for det pågældende ciffer.
- Trin3: Læg alle de tal sammen, der er opnået efter multiplikation i det foregående trin.
- Trin4: Det tal, der er opnået i sidste trin, er decimalækvivalenten af oktaltallet.
Eksempel: Lad os tage et oktaltal 1265 i betragtning.