Hur konverterar man mellan oktal- och decimaltalsystem?
Innan vi går in på hur man omvandlar ett talsystem till ett annat, låt oss tala lite om själva talsystemet. Talssystemet kan definieras som en uppsättning olika kombinationer av symboler, där varje symbol har en specifik vikt. Alla talsystem skiljer sig åt på grundval av radix eller den bas som talsystemet bygger på. Radix eller basen definierar det totala antalet olika symboler som används i ett visst talsystem. Exempelvis är radix i det binära talsystemet 2, radix i det decimala talsystemet 10 och radix i det oktala talsystemet 8.
Det oktala talsystemet:
Som namnet tydligt visar är detta talsystem baserat på en radx som är lika med 8. I detta talsystem har vi alltså åtta olika siffror. För enkelhetens skull betraktar vi dessa åtta siffror som samma som de första åtta siffrorna i decimaltalsystemet. Varje oktalsiffras position är associerad med en potens av 8 och denna potens är lika med indexet för siffran från vänster position. Det krävs högst tre binära siffror för att representera ett oktaltal i binär form. Eftersom basen för detta talsystem i sig är en potens av två är det mycket enkelt och bekvämt att omvandla oktalsiffror till binära eller hexadecimala talsystem som används i datorer för att utföra allt arbete.
Oktaltal kan inte användas direkt i datamaskineriet eftersom datorer arbetar med binära tillstånd eller bitar. Eftersom oktalsiffrorna har färre siffror att representera i binär form kan de dock lagras effektivt i datorn utan att det går åt något slöseri med utrymme i minnet som BCD-nummer (binärt kodade decimala tal).
Konvertering av decimaltal till oktaltal:
Omvandlingen av decimal till oktal är mycket lik den som sker när man omvandlar decimal till binär. Den enda skillnaden är att vi den här gången delar decimaltalet med 8 i stället för 2. Konverteringen kan göras genom att följa nedanstående steg:
- Steg 1: Dividera decimaltalet med 8, notera återstoden och tilldela den värdet R1. På samma sätt noterar du kvoten och tilldelar den värdet Q1.
- Steg2: Dela nu Q1 med 8, notera återstoden och kvoten. Tilldela värdet R2 och Q2 till den rest och kvot som erhållits i detta steg.
- Steg3: Upprepa sekvensen tills du får ett kvotvärde (Qn) som är lika med 0.
- Steg4: Oktalnumret kommer att se ut ungefär så här: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Exempel: Låt oss betrakta ett decimaltal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
OCTAL motsvarigheten till 2181 är alltså:
(2181) Decimal = (4205) Octal
Konvertering av oktal till binärt talsystem:
Återigen är konverteringen av oktal till decimal mycket lik konverteringen av binär till decimal, den enda skillnaden är att den här gången multiplicerar vi siffrorna med potenser av 8 i stället för 2. Konverteringen kan göras genom att följa nedanstående steg:
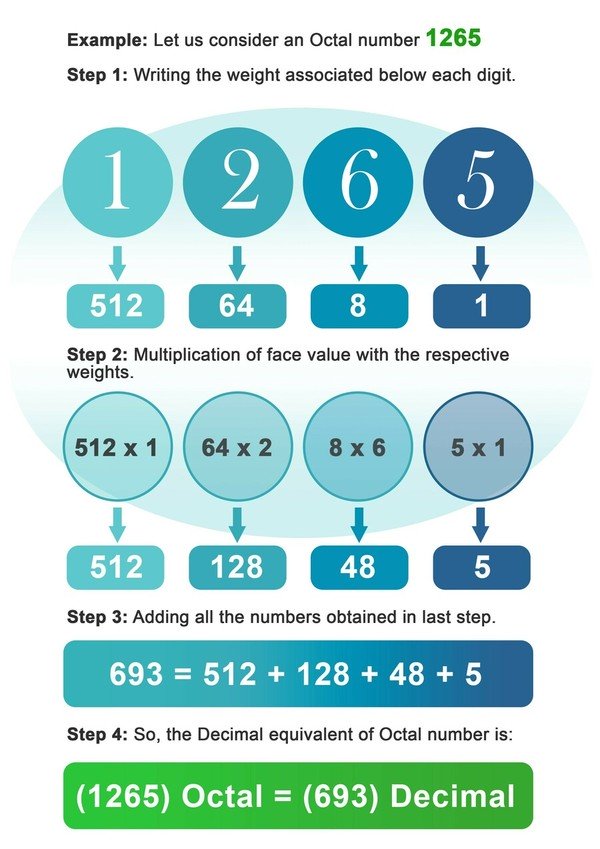
- Steg 1: Skriv ner vikten av 8 under varje siffra i oktaltalet.
- Steg 2: Multiplicera nu varje siffra med den vikt som är kopplad till den platsen eller indexet för siffran.
- Steg3: Addera alla de tal som erhållits efter multiplikation i föregående steg.
- Steg 4: Det tal som erhålls i det sista steget är decimalekvivalenten till oktaltalet.
Exempel: Låt oss betrakta oktaltalet 1265.