Wie konvertiert man zwischen dem Oktal- und Dezimalzahlsystem?
Bevor wir uns mit der Umwandlung eines Zahlensystems in ein anderes befassen, wollen wir ein wenig über das Zahlensystem selbst sprechen. Das Zahlensystem kann definiert werden als die Menge der verschiedenen Kombinationen von Symbolen, wobei jedes Symbol ein bestimmtes Gewicht hat. Jedes Zahlensystem wird auf der Grundlage des Radix oder der Basis, auf der das Zahlensystem aufgebaut ist, unterschieden. Das Radix oder die Basis definiert die Gesamtzahl der verschiedenen Symbole, die in einem bestimmten Zahlensystem verwendet wird. Zum Beispiel ist die Radix des binären Zahlensystems 2, die Radx des dezimalen Zahlensystems 10 und die Radx des oktalen Zahlensystems 8.
Das Oktalzahlensystem:
Wie der Name schon sagt, basiert dieses Zahlensystem auf Radix gleich 8. In diesem Zahlensystem haben wir also acht verschiedene Ziffern. Der Einfachheit halber betrachten wir diese acht Ziffern als die ersten acht Ziffern des dezimalen Zahlensystems. Die Position jeder Oktalziffer ist mit einer Potenz von 8 verbunden, und diese Potenz entspricht dem Index der Ziffer von der linken Position aus. Es sind maximal drei Binärziffern erforderlich, um eine Oktalzahl in binärer Form darzustellen. Da die Basis dieses Zahlensystems selbst eine Zweierpotenz ist, ist es sehr einfach und bequem, Oktalzahlen in binäre oder hexadezimale Zahlensysteme umzuwandeln, die in Computern verwendet werden, um die gesamte Arbeit zu erledigen.
Oktalzahlen finden in der Computermaschinerie keine direkte Anwendung, weil Computer auf binären Zuständen oder Bits arbeiten. Da die Oktalzahl jedoch weniger Ziffern belegt, um binär dargestellt zu werden, können sie effizient im Computer gespeichert werden, ohne dass wie bei der BCD(Binary Coded Decimal)-Zahl Platz im Speicher verschwendet wird.
Umwandlung von Dezimal- in Oktalzahlensystem:
Die Umwandlung von Dezimal in Oktal ist der Umwandlung von Dezimal in Binär sehr ähnlich. Der einzige Unterschied ist, dass wir diesmal die Dezimalzahl durch 8 statt durch 2 teilen. Die Konvertierung kann mit den unten beschriebenen Schritten durchgeführt werden:
- Schritt 1: Dividieren Sie die Dezimalzahl durch 8, notieren Sie den Rest und weisen Sie ihm den Wert R1 zu. In ähnlicher Weise notieren Sie den Quotienten und weisen ihm den Wert Q1 zu.
- Schritt 2: Teilen Sie nun Q1 durch 8, notieren Sie den Rest und den Quotienten. Weisen Sie dem in diesem Schritt erhaltenen Rest und Quotienten den Wert R2 und Q2 zu.
- Schritt 3: Wiederholen Sie die Sequenz, bis Sie den Wert des Quotienten (Qn) gleich 0 erhalten.
- Schritt 4: Die Oktalzahl wird etwa so aussehen: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Beispiel: Betrachten wir eine Dezimalzahl 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Das OCTAL-Äquivalent von 2181 ist also:
(2181) Decimal = (4205) Octal
Umwandlung des Oktal- in ein binäres Zahlensystem:
Auch hier ist die Konvertierung von Oktal in Dezimal sehr ähnlich der Konvertierung von Binär in Dezimal, der einzige Unterschied besteht darin, dass wir diesmal die Ziffern mit den Potenzen von 8 statt 2 multiplizieren:
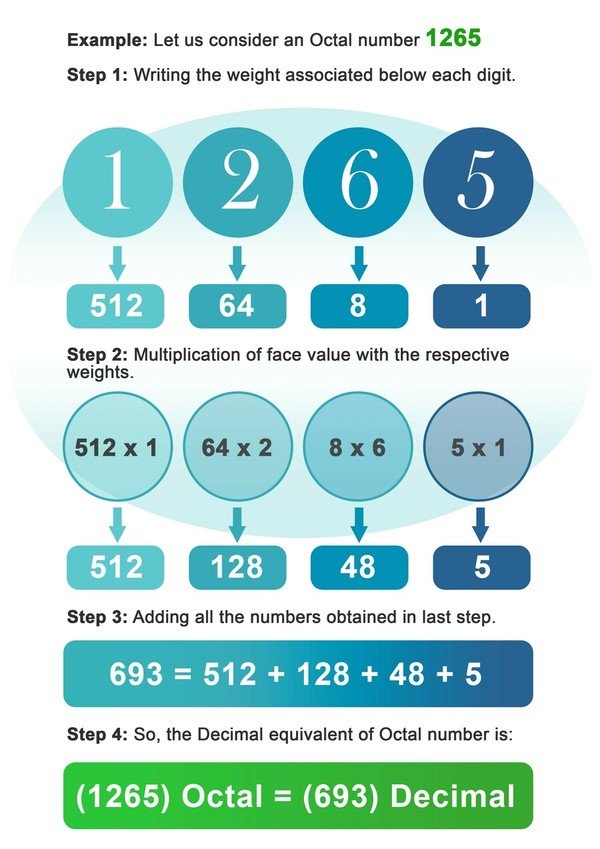
- Schritt 1: Notieren Sie das Gewicht der 8, die unter jeder Ziffer der Oktalzahl steht.
- Schritt 2: Multiplizieren Sie nun jede Ziffer mit dem Gewicht, das an dieser Stelle oder dem Index der Ziffer zugeordnet ist.
- Schritt 3: Addieren Sie alle Zahlen, die Sie nach der Multiplikation im vorherigen Schritt erhalten haben.
- Schritt 4: Die im letzten Schritt erhaltene Zahl ist das dezimale Äquivalent der Oktalzahl.
Beispiel: Betrachten wir eine Oktalzahl 1265.