Jak převádět mezi osmičkovou a desítkovou číselnou soustavou?
Než se pustíme do rozhovoru o převodu jedné číselné soustavy na druhou, řekněme si něco o samotné číselné soustavě. Číselnou soustavu lze definovat jako soubor různých kombinací symbolů, přičemž každý symbol má určitou váhu. Každá číselná soustava se rozlišuje na základě radixu neboli základu, na kterém je číselná soustava vytvořena. Radix nebo základ definuje celkový počet různých symbolů, které se v dané číselné soustavě používají. Například radix binární číselné soustavy je 2, radix desítkové číselné soustavy je 10 a radix osmičkové číselné soustavy je 8.
Osmičková číselná soustava:
Jak název jasně naznačuje, tato číselná soustava je založena na radixu rovném 8. V této číselné soustavě tedy máme osm různých číslic. Pro zjednodušení považujeme těchto osm číslic za stejných jako prvních osm číslic v desítkové číselné soustavě. Pozice každé osmičkové číslice je spojena s určitou mocninou čísla 8 a tato mocnina se rovná indexu číslice od levé pozice. K vyjádření jednoho osmičkového čísla ve dvojkové soustavě jsou zapotřebí maximálně tři binární číslice. Protože základem této číselné soustavy je mocnina dvojky, je velmi snadné a pohodlné převádět osmičková čísla do binární nebo šestnáctkové číselné soustavy, které se používají v počítačích ke všem činnostem.
Osmičková čísla nenajdou přímé uplatnění v počítačové technice, protože počítače pracují s binárními stavy nebo bity. Protože však osmičková čísla zabírají méně číslic, které je třeba reprezentovat v binární soustavě, mohou být efektivně uložena v počítači bez zbytečného místa v paměti jako čísla BCD (Binary Coded Decimal).
Převod desítkové číselné soustavy na osmičkovou:
Převod desítkové soustavy na osmičkovou je velmi podobný převodu desítkové soustavy na dvojkovou. Jediný rozdíl je v tom, že tentokrát budeme desítkové číslo dělit číslem 8 namísto 2. Převod lze provést podle níže napsaných kroků:
- Krok1: Vydělte desetinné číslo číslem 8, zapište zbytek a přiřaďte mu hodnotu R1. Podobně si zapište kvocient a přiřaďte mu hodnotu Q1.
- Krok2: Nyní vydělte Q1 číslem 8, zapište zbytek a kvocient. Zbytku a kvocientu získanému v tomto kroku přiřaďte hodnoty R2 a Q2.
- Krok3: Postup opakujte, dokud se hodnota kvocientu (Qn) nebude rovnat 0.
- Krok4: Osmičkové číslo bude vypadat takto: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Příklad: Uvažujme desetinné číslo 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Ekvivalent OCTAL pro 2181 je tedy:
(2181) Decimal = (4205) Octal
Převod osmičkové do dvojkové číselné soustavy:
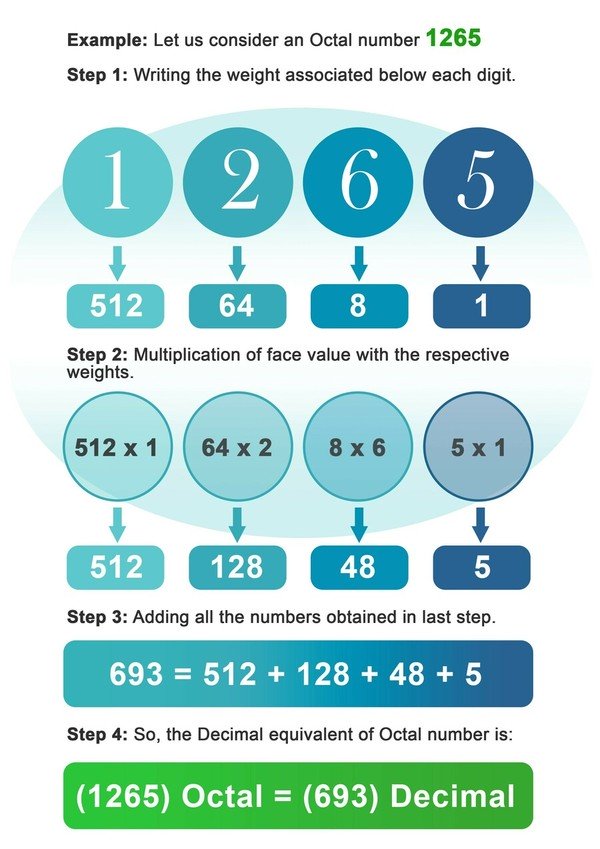
Převod osmičkové soustavy na desítkovou je opět velmi podobný převodu dvojkové soustavy na desítkovou, jen s tím rozdílem, že tentokrát budeme číslice násobit mocninami 8 místo 2. Převod lze provést podle níže napsaných kroků:
- Krok 1: Zapište váhu 8 přiřazenou pod každou číslici osmičkového čísla.
- Krok2: Nyní vynásobte každou číslici váhou přiřazenou danému místu nebo indexu číslice.
- Krok3: Sečtěte všechna čísla získaná po vynásobení v předchozím kroku.
- Krok4: Číslo získané vposledním kroku je desítkovým ekvivalentem osmičkového čísla.
Příklad: Uvažujme osmičkové číslo 1265.