Як перетворити числа між вісімковою та десятковою числовими системами?
Перш ніж перейти до розмови про перетворення однієї числової системи на іншу, давайте трохи поговоримо про саму числову систему. Числову систему можна визначити як набір різних комбінацій символів, при цьому кожен символ має певну вагу. Будь-яку числову систему відрізняють за основою або базою, на якій побудована числова система. Основа або база визначає загальну кількість різних символів, які використовуються у певній числовій системі. Наприклад, основа двійкової числової системи - 2, десяткової числової системи - 10, а восьмиркової числової системи - 8.
Система вісімкових чисел:
Як сама назва вказує, ця числова система базується на основі, рівній 8. Таким чином, в цій числовій системі ми маємо вісім різних цифр. Для зручності ми вважаємо ці вісім цифр такими самими, як перші вісім цифр у десятковій числовій системі. Положення кожної восьмирічної цифри пов'язане з деякою степенем числа 8, а ця степінь дорівнює індексу цифри з лівого положення. Для представлення одного восьмиричного числа у двійковій формі потрібно не більше ніж три двійкові цифри. Оскільки основа цієї числової системи сама є деякою степенню двійки, то дуже легко і зручно взаємозамінювати восьмиричне число у двійкову або шістнадцятирічну числову системи, які використовуються в комп'ютерах для виконання всіх робіт.
Восьмиричні числа не мають прямого застосування в обчислювальних механізмах, оскільки комп'ютери працюють з двійковими станами або бітами. Однак, оскільки восьмиричне число займає менше розрядів для представлення у двійковій системі, воно може бути ефективно збережене в комп'ютері без витрачання зайвого простору в пам'яті, як у двійковому кодованому десятковому числі (BCD).
Перетворення десяткової на вісімкову чисельну систему:
Перетворення десяткового числа на вісімкове дуже схоже на перетворення десяткового числа на двійкове. Єдине відмінність полягає в тому, що цього разу ми будемо ділити десяткове число на 8 замість 2. Перетворення можна виконати, дотримуючись написаних нижче кроків:
- Крок 1: Розділити десяткове число на 8, відмітити залишок і призначити йому значення R1. Аналогічно, відмітити частку і призначити йому значення Q1.
- Крок 2: Тепер ділимо Q1 на 8, залишок і частку позначаємо як R2 та Q2.
- Крок 3: Повторіть послідовність, доки значення частки (Qn) не стане рівним 0.
- Крок 4: Восьмеричне число матиме вигляд, схожий на цей : Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Приклад: Розглянемо десяткове число 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Отже, вісімковий еквівалент числа 2181:
(2181) Decimal = (4205) Octal
Перетворення з вісімкової в двійкову систему числення:
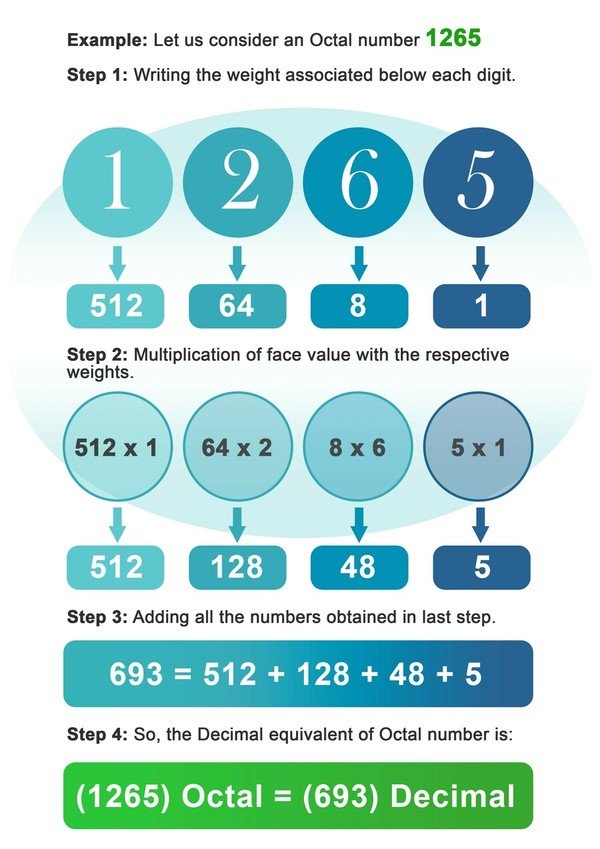
Знову, конвертація вісімкового числа в десяткове число дуже схожа на конвертацію двійкового числа в десяткове, є лише одна відмінність - на цей раз ми будемо множити цифри на степені 8 замість 2. Конвертацію можна виконати, дотримуючись нижче наведених кроків:
- Крок 1: Запишіть вагу 8 асоційованих нижче кожної цифри вісімкового числа.
- Крок 2: Тепер помножте кожну цифру на вагу, пов'язану з цим місцем або індексом цифри.
- Крок 3: Додайте всі числа, отримані після множення на попередньому кроці.
- Крок 4: Число, отримане на останньому кроці, є десятковим еквівалентом вісімкового числа.
Приклад: Розглянемо вісімкове число 1265.