Comment convertir entre le système des nombres octal et décimal ?
Avant d'entrer dans la conversation sur la conversion d'un système de numéros en un autre, parlons un peu du système de numéros lui-même. Le système de numérotation peut être défini comme l'ensemble des différentes combinaisons de symboles, chaque symbole ayant un poids spécifique. Tout système de numérotation se différencie par le rayon ou la base sur laquelle il est fabriqué. Le radix ou la base définit le nombre total de symboles différents, qui est utilisé dans un système de nombres particulier. Par exemple, le rayon du système de nombres binaires est 2, le rayon du système de nombres décimaux est 10, et le rayon du système de nombres octal est 8.
Le système de numérotation octal :
Comme son nom l'indique clairement, ce système de numérotation est basé sur un rayon égal à 8. Ainsi, dans ce système de numérotation, nous avons huit chiffres distincts. Pour plus de facilité, nous considérons ces huit chiffres comme étant les mêmes que les huit premiers chiffres du système de numérotation décimale. La position de chaque chiffre octal est associée à une certaine puissance de 8 et cette puissance est égale à l'index du chiffre à partir de la position gauche. Il faut au maximum trois chiffres binaires pour représenter un nombre octal sous forme binaire. Comme la base de ce système de nombres est elle-même une puissance de deux, il est très facile et pratique d'interconvertir un nombre octal en un système de nombres binaires ou hexadécimaux qui sont utilisés dans les ordinateurs pour faire tout le travail.
Les nombres octals ne trouvent pas d'application directe dans la machinerie informatique car les ordinateurs fonctionnent sur des états binaires ou des bits. Cependant, comme les nombres octals occupent moins de chiffres pour être représentés en binaire, ils peuvent être stockés efficacement dans l'ordinateur sans perte d'espace en mémoire comme le nombre BCD (Binary Coded Decimal).
Conversion du système de nombres décimaux en nombres octaux :
La conversion de décimal en octal est très similaire à la conversion de décimal en binaire. La seule différence est que cette fois, nous allons diviser le nombre décimal par 8 au lieu de 2. La conversion peut être effectuée en suivant les étapes écrites ci-dessous :
- Étape 1 : Divisez le nombre décimal par 8, notez le reste et attribuez-lui la valeur R1. De même, notez le quotient et attribuez-lui la valeur Q1.
- Étape 2 : Divisez maintenant Q1 par 8, notez le reste et le quotient. Attribuez la valeur R2 et Q2 au reste et au quotient obtenus à cette étape.
- Étape 3 : Répétez la séquence jusqu'à ce que vous obteniez la valeur du quotient (Qn) égale à 0.
- Étape 4 : Le nombre octal ressemblera à ceci: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Exemple : Considérons un nombre décimal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Ainsi, l'équivalent OCTAL de 2181 est :
(2181) Decimal = (4205) Octal
Conversion de l'octal en système de nombres binaires :
Là encore, la conversion de l'octal en décimal est très similaire à la conversion du binaire en décimal, la seule différence est que cette fois nous allons multiplier les chiffres avec les puissances de 8 au lieu de 2. La conversion peut être effectuée en suivant les étapes écrites ci-dessous :
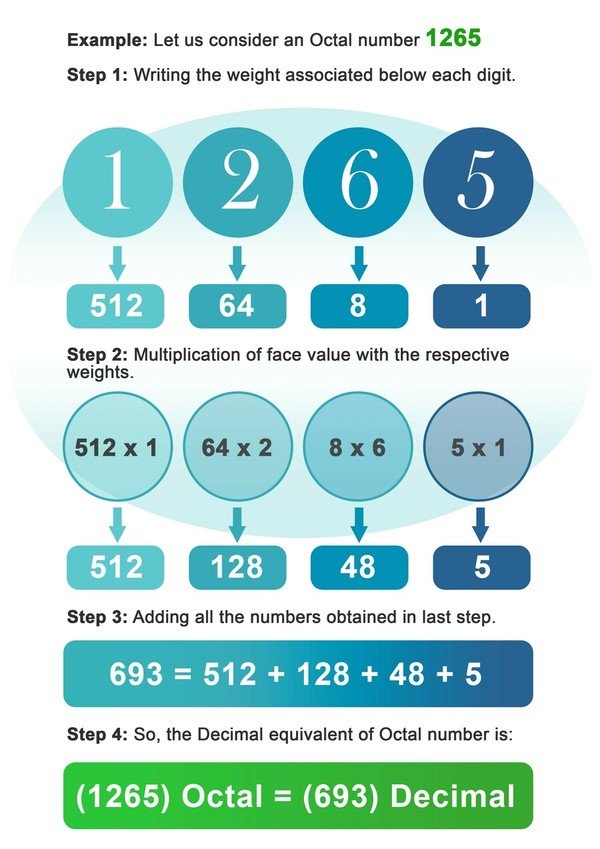
- Étape 1 : Inscrivez le poids de 8 associé sous chaque chiffre du nombre octal.
- Étape 2 : Multipliez maintenant chaque chiffre par le poids associé à cet endroit ou à cet indice de chiffre.
- Étape 3 : Additionner tous les nombres obtenus après multiplication à l'étape précédente.
- Étape 4 : Le nombre obtenu à la dernière étape est l'équivalent décimal du nombre octal.
Exemple : Considérons un nombre octal 1265.