Kuinka muuntaa oktaali- ja desimaalilukujärjestelmän välillä?
Ennen kuin alamme keskustella yhden numerojärjestelmän muuntamisesta toiseen, puhutaan hieman itse numerojärjestelmästä. Numerojärjestelmä voidaan määritellä symbolien erilaisten yhdistelmien joukoksi, jossa kullakin symbolilla on tietty painoarvo. Mikä tahansa numerojärjestelmä erotetaan toisistaan radeksin eli sen perusteella, mihin peruslukuun numerojärjestelmä perustuu. Radiksi tai perusta määrittelee eri symbolien kokonaismäärän, jota tietyssä numerojärjestelmässä käytetään. Esimerkiksi binäärilukujärjestelmän radix on 2, desimaalilukujärjestelmän radix on 10 ja oktaalilukujärjestelmän radix on 8.
Oktal-lukujärjestelmä:
Kuten nimikin selvästi osoittaa, tämä lukujärjestelmä perustuu radixiin 8. Tässä numerojärjestelmässä on siis kahdeksan erillistä numeroa. Yksinkertaisuuden vuoksi katsomme, että nämä kahdeksan numeroa ovat samat kuin desimaalilukujärjestelmän kahdeksan ensimmäistä numeroa. Jokaisen oktaaliluvun sijaintiin liittyy jokin 8:n potenssi, ja tämä potenssi vastaa numeron indeksiä vasemmalta puolelta. Yhden oktaaliluvun esittämiseen binäärimuodossa tarvitaan enintään kolme binäärinumeroa. Koska tämän lukujärjestelmän perusta on jokin potenssi kahdesta, on erittäin helppoa ja kätevää muuntaa oktaaliluku binääri- tai heksadesimaalilukujärjestelmään, jota käytetään tietokoneissa kaiken työn tekemiseen.
Oktalilukuja ei käytetä suoraan tietokonekoneissa, koska tietokoneet toimivat binääritilojen tai bittien avulla. Koska kahdeksasluvussa on kuitenkin vähemmän binäärilukuna esitettäviä numeroita, ne voidaan tallentaa tehokkaasti tietokoneeseen ilman turhaa muistitilaa, kuten BCD (Binary Coded Decimal) -luvut.
Desimaalilukujärjestelmän muuntaminen oktaalilukujärjestelmään:
Desimaaliluvun muuntaminen oktaaliluvuksi on hyvin samanlaista kuin desimaaliluvun muuntaminen binääriluvuksi. Ainoa ero on, että tällä kertaa jaamme desimaaliluvun 8:lla eikä 2:lla. Muunnos voidaan tehdä noudattamalla alla olevia ohjeita:
- Vaihe1: Jaa desimaaliluku luvulla 8, merkitse jäännös ja anna sille arvo R1. Vastaavasti merkitään muistiin osamäärä ja annetaan sille arvo Q1.
- Vaihe2: Jaa nyt Q1 luvulla 8, merkitse jäännös ja osamäärä. Määritä tässä vaiheessa saatujen jäännös- ja osamääräarvojen R2 ja Q2 arvot.
- Vaihe 3: Toista sarjaa, kunnes saat osamäärän (Qn) arvoksi 0.
- Vaihe4: Oktal-luku näyttää jotakuinkin tältä.: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Esimerkki: Tarkastellaan desimaalilukua 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
OCTAL-ekvivalentti 2181 on siis:
(2181) Decimal = (4205) Octal
Octal-järjestelmän muuntaminen binäärilukujärjestelmäksi:
Jälleen kerran oktaaliluvun muuntaminen desimaaliluvuksi on hyvin samanlaista kuin binääriluvun muuntaminen desimaaliluvuksi, ainoa ero on, että tällä kertaa numerot kerrotaan potensseilla 8 eikä 2. Muunnos voidaan tehdä noudattamalla alla olevia ohjeita:
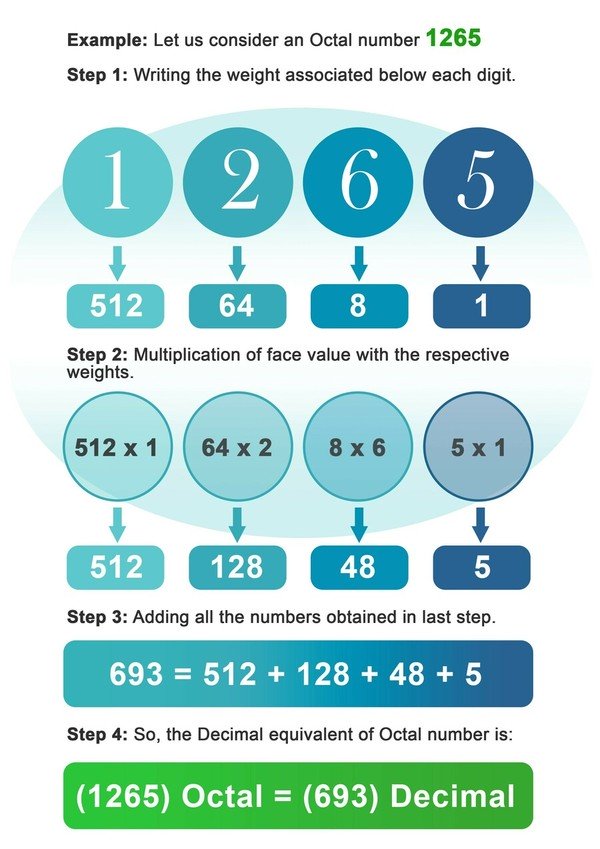
- Vaihe 1: Kirjoita ylös kahdeksan paino, joka liittyy oktaaliluvun jokaisen numeron alle.
- Vaihe2: Kerro nyt jokainen numero kyseiseen paikkaan tai numeron indeksiin liittyvällä painolla.
- Vaihe 3: Lasketaan yhteen kaikki edellisen vaiheen kertolaskun jälkeen saadut luvut.
- Vaihe 4: Viimeisessä vaiheessa saatu luku on kahdeksasluvun desimaaliluku.
Esimerkki: 1265.