八進法と十進法の変換方法は?
他の番号システムへの変換の話に入る前に、私たちは番号システム自体について少し話をしてみましょう。数字システムは、記号の異なる組み合わせの集合として定義することができ、各記号は特定の重みを持っています。どのような番号システムも、その番号システムが作られている基数またはベースに基づいて区別されています。基数またはベースは、特定の番号システムで使用されている異なるシンボルの合計数を定義します。例えば、2進数系の基数は2、10進数系の基数は10、8進数系の基数は8です。
八進数システム。
名前が明確に示すように、この数システムは8に等しい基数に基づいています。だから、この数システムでは、我々は8つの明確な数字を持っています。簡単にするために、我々は10進数システムの最初の8桁と同じように、これらの8桁を考慮してください。各8進数桁の位置は、8のいくつかの乗に関連付けられており、この乗は、左の位置から桁のインデックスに等しい。2進数で1つの8進数を表現するには、最大で3桁の2進数が必要です。この数システム自体のベースは2のいくつかの力であるので、それはすべての作業を行うためにコンピュータで使用されている2進数または16進数システムに8進数を相互変換することは非常に簡単で便利です。
コンピュータはバイナリ状態またはビットで動作するため、八進数は、コンピュータの機械で直接アプリケーションを見つけることはありません。しかし、八進数は、彼らが効率的にBCD(二進コード10進数)番号のようなメモリ内の任意の無駄なスペースを使用せずにコンピュータに格納することができますので、バイナリで表現するためのより少ない桁を占有するように。
10進数から10進数への変換。
10進数から8進数への変換は、10進数を2進数に変換するのと非常に似ています。唯一の違いは、今回は10進数を2ではなく8で割ることです。 変換は以下の手順で行うことができます。
- Step1: 10進数を8で割って、余った分をメモして、それに値R1を代入する。同様に、商をメモして、値Q1を代入する。
- Step2: Q1を8で割って、余りと商に注意してください。このステップで得られた余りと商に値R2とQ2を代入する。
- Step3: 商(Qn)の値が0になるまで繰り返します。
- ステップ4:8進数は次のようになります。: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
例を挙げてみます。 10進数2181を考えてみましょう。
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
つまり、2181のOCTAL相当は
(2181) Decimal = (4205) Octal
八進数を二進数系に変換します。
繰り返しになりますが、8進数から10進数への変換は、2進数から10進数への変換と非常に似ています。 唯一の違いは、今回は2の代わりに8の累乗で桁を乗算するということです。 変換は、以下のように書かれた手順を実行することで行うことができます。
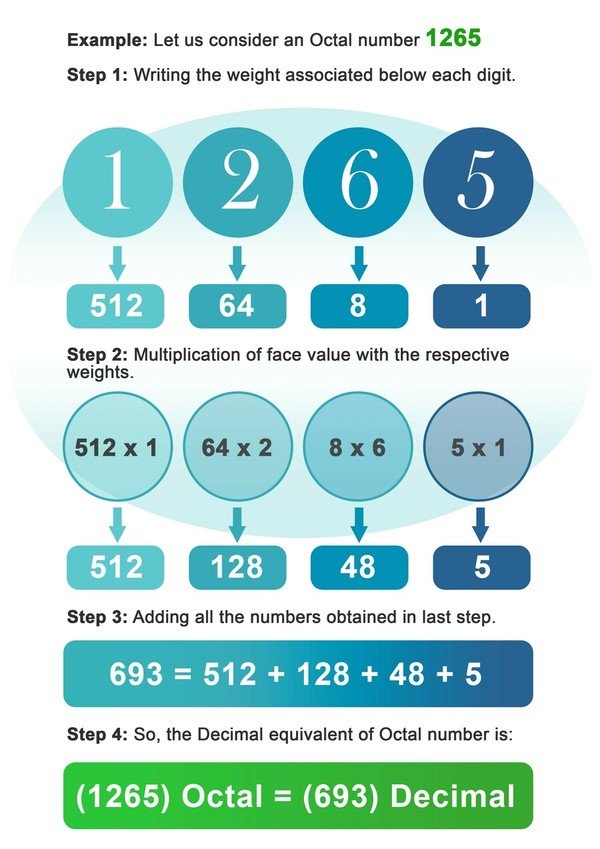
- ステップ1:8進数の各桁の下にある8の重さを書きます。
- Step2: 各桁に、その場所または桁のインデックスに関連付けられた重みを掛けます。
- Step3:前のステップで掛け算をして得た数字をすべて足し算します。
- Step4:最後のステップで得られた数値は、8進数の10進数換算値である。
例.オクタル数1265を考えてみましょう。