Hogyan konvertáljunk az oktális és a tizedes számrendszerek között?
Mielőtt belemennénk az egyik számrendszer átváltásáról a másikra, beszéljünk egy kicsit magáról a számrendszerről. A számrendszert úgy határozhatjuk meg, mint a szimbólumok különböző kombinációinak halmazát, ahol minden szimbólumnak meghatározott súlya van. Minden számrendszert megkülönböztetünk a radix vagy az alap alapján, amelyre a számrendszer épül. A radix vagy a bázis határozza meg az adott számrendszerben használt különböző szimbólumok teljes számát. Például a bináris számrendszer radixa 2, a decimális számrendszer radixa 10, a nyolcjegyű számrendszer radixa pedig 8.
Az oktális számrendszer:
Ahogy a neve is egyértelműen jelzi, ez a számrendszer a 8-as radixon alapul. Ebben a számrendszerben tehát nyolc különböző számjegy van. Az egyszerűség kedvéért ezt a nyolc számjegyet a tizedes számrendszer első nyolc számjegyének tekintjük. Minden egyes nyolcjegyű számjegy pozíciójához a 8 valamelyik hatványa tartozik, és ez a hatvány megegyezik a számjegy indexével a bal oldali pozíciótól. Egy nyolcjegyű szám bináris formában történő ábrázolásához legfeljebb három bináris számjegy szükséges. Mivel ennek a számrendszernek az alapja maga is valamilyen kettes hatvány, ezért nagyon könnyű és kényelmes a nyolcjegyű számok bináris vagy hexadecimális számrendszerbe való átváltása, amelyet a számítógépek minden munkához használnak.
Az oktális számok nem találnak közvetlen alkalmazást a számítógépes gépekben, mivel a számítógépek bináris állapotokkal vagy bitekkel dolgoznak. Mivel azonban a nyolcjegyű számok kevesebb számjegyet foglalnak el a bináris ábrázoláshoz, így hatékonyan tárolhatók a számítógépben, a memóriában elvesztegetett hely nélkül, mint a BCD (Binary Coded Decimal) számok.
A decimális számrendszer átalakítása oktális számrendszerré:
A decimális számrendszer oktálisra történő átalakítása nagyon hasonló a decimális számrendszer binárisra történő átalakításához. Az egyetlen különbség az, hogy ezúttal a decimális számot 2 helyett 8-cal osztjuk. Az átalakítás az alábbiakban leírt lépéseket követve végezhető el:
- 1. lépés: Osszuk el a tizedes számot 8-cal, jegyezzük fel a maradékot, és rendeljük hozzá az R1 értéket. Hasonlóképpen jegyezzük fel a hányadost, és rendeljük hozzá a Q1 értéket.
- 2. lépés: Most osszuk el a Q1-et 8-cal, jegyezzük fel a maradékot és a hányadost. Az ebben a lépésben kapott maradékhoz és hányadoshoz rendeljük hozzá az R2 és Q2 értéket.
- 3. lépés: Ismételje meg a sorozatot, amíg a hányados (Qn) értéke 0-nak nem felel meg.
- 4. lépés: A nyolcjegyű szám így fog kinézni: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Példa: Tekintsük a 2181-es tizedes számot.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Tehát a 2181 OCTAL-egyenértéke a következő:
(2181) Decimal = (4205) Octal
Az oktális számrendszer átalakítása bináris számrendszerré:
A nyolcjegyű számjegyek decimálisra történő átalakítása ismét nagyon hasonló a bináris számjegyek decimálisra történő átalakításához, az egyetlen különbség az, hogy ezúttal a számjegyeket 2 helyett 8-as hatványokkal szorozzuk. Az átalakítás az alábbiakban leírt lépésekkel végezhető el:
- 1. lépés: Írja le a nyolcas szám minden számjegye alá a 8-as súlyát.
- 2. lépés: Most szorozzuk meg az egyes számjegyeket az adott helyhez vagy a számjegy indexéhez tartozó súllyal.
- 3. lépés: Adjuk össze az előző lépésben elvégzett szorzás után kapott számokat.
- 4. lépés: Az utolsó lépésben kapott szám a nyolcjegyű szám tizedes egyenértéke.
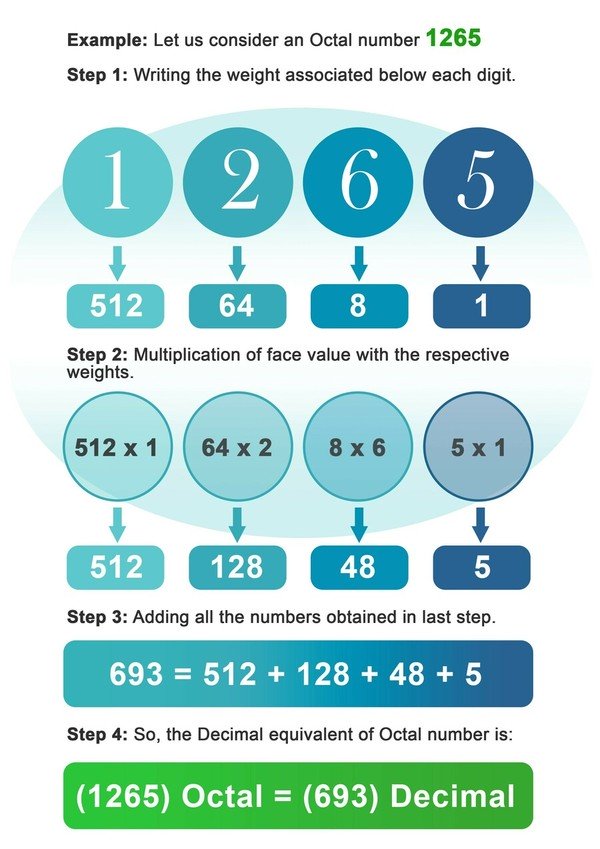
Példa: Tekintsük az 1265-ös oktális számot.