Как да конвертираме между осмична и десетична бройна система?
Преди да започнем разговора за преобразуването на една бройна система в друга, нека поговорим малко за самата бройна система. Цифровата система може да се определи като набор от различни комбинации от символи, като всеки символ има определена тежест. Всяка бройна система се разграничава въз основа на радикса или основата, върху която е изградена бройната система. Радиксът или базата определят общия брой на различните символи, които се използват в дадена бройна система. Например радиксът на двоичната бройна система е 2, радиксът на десетичната бройна система е 10, а радиксът на осмичната бройна система е 8.
Октална бройна система:
Както ясно показва името, тази бройна система се основава на радикс, равен на 8. Така че в тази бройна система имаме осем различни цифри. За улеснение ще разглеждаме тези осем цифри като същите като първите осем цифри в десетичната бройна система. Позицията на всяка осмична цифра е свързана с някаква степен на 8 и тази степен е равна на индекса на цифрата от лявата позиция. За представянето на едно осмично число в двоична форма са необходими най-много три двоични цифри. Тъй като самата основа на тази бройна система е някаква степен на две, е много лесно и удобно да се преобразуват осмичните числа в двоична или шестнадесетична бройна система, които се използват в компютрите за извършване на цялата работа.
Окталните числа не намират пряко приложение в компютърната техника, тъй като компютрите работят с двоични състояния или битове. Въпреки това, тъй като осемцифрените числа заемат по-малко цифри за представяне в двоична система, те могат да се съхраняват ефективно в компютъра, без да се губи място в паметта, както BCD (двоично кодирано десетично число).
Преобразуване на десетична в осмична бройна система:
Преобразуването на десетична в осмична система е много подобно на преобразуването на десетична в двоична система. Единствената разлика е, че този път ще разделим десетичното число с 8 вместо с 2. Преобразуването може да се извърши, като следвате написаните по-долу стъпки:
- Стъпка 1: Разделете десетичното число на 8, запишете остатъка и му присвоете стойността R1. По същия начин запишете коефициента и му присвоете стойността Q1.
- Стъпка 2: Сега разделете Q1 на 8, запишете остатъка и коефициента. Присвоете стойностите R2 и Q2 на остатъка и коефициента, получени в тази стъпка.
- Стъпка 3: Повтаряйте последователността, докато получите стойност на коефициента (Qn), равна на 0.
- Стъпка4: Окталното число ще изглежда по следния начин: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Пример: Нека разгледаме десетично число 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Така че еквивалентът на 2181 по OCTAL е:
(2181) Decimal = (4205) Octal
Преобразуване на осмична в двоична бройна система:
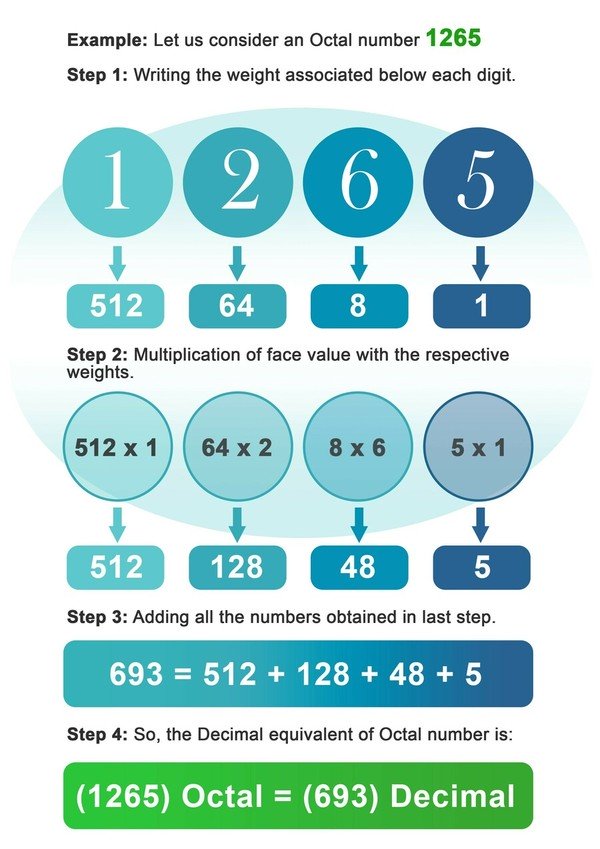
Отново преобразуването на осмична в десетична система е много подобно на преобразуването на двоична в десетична система, с единствената разлика, че този път ще умножим цифрите със степен 8 вместо с 2. Преобразуването може да се извърши, като се следват написаните по-долу стъпки:
- Стъпка 1: Запишете теглото на 8, свързано под всяка цифра на осмичното число.
- Стъпка 2: Сега умножете всяка цифра с теглото, свързано с това място или индекс на цифрата.
- Стъпка 3: Съберете всички числа, получени след умножението в предишната стъпка.
- Стъпка4: Числото, получено в последната стъпка, е десетичният еквивалент на осмичното число.
Пример: Нека разгледаме осемцифрено число 1265.