Cum se face conversia între sistemele numerice octal și zecimal?
Înainte de a intra în discuția despre conversia unui sistem numeric în altul, să vorbim puțin despre sistemul numeric în sine. Sistemul numeric poate fi definit ca fiind ansamblul diferitelor combinații de simboluri, fiecare simbol având o pondere specifică. Orice Sistem Numeric se diferențiază pe baza radixului sau a bazei pe care este realizat sistemul numeric. Radixul sau baza definește numărul total de simboluri diferite, care este utilizat într-un anumit sistem de numere. De exemplu, radixul sistemului de numere binare este 2, radixul sistemului de numere zecimale este 10, iar radixul sistemului de numere octale este 8.
Sistemul numeric octal:
După cum indică în mod clar numele, acest sistem numeric se bazează pe un radix egal cu 8. Așadar, în acest sistem numeric avem opt cifre distincte. Pentru ușurință, considerăm că aceste opt cifre sunt identice cu primele opt cifre din sistemul de numerație zecimal. Poziția fiecărei cifre octale este asociată cu o anumită putere a lui 8, iar această putere este egală cu indicele cifrei din poziția din stânga. Sunt necesare cel mult trei cifre binare pentru a reprezenta un număr octal în formă binară. Deoarece baza acestui sistem de numere este o putere de 2, este foarte ușor și convenabil să se interconvertească numerele octale în sistemul binar sau hexazecimal, care sunt utilizate în calculatoare pentru a efectua toate operațiile.
Numerele octale nu se aplică direct în mașinile de calculatoare, deoarece calculatoarele lucrează pe baza stărilor binare sau a biților. Cu toate acestea, întrucât numerele octale ocupă mai puține cifre pentru a fi reprezentate în binar, ele pot fi stocate eficient în calculator fără a pierde spațiu în memorie, la fel ca numerele BCD (Binary Coded Decimal).
Conversia sistemului numeric zecimal în sistem numeric octal:
Conversia din zecimal în octal este foarte asemănătoare cu conversia din zecimal în binar. Singura diferență este că, de data aceasta, vom împărți numărul zecimal cu 8 în loc de 2. Conversia se poate face urmând pașii scriși mai jos:
- Pasul 1: Se împarte numărul zecimal cu 8, se notează restul și i se atribuie valoarea R1. În mod similar, notați cutientul și atribuiți-i valoarea Q1.
- Pasul 2: Acum împărțiți Q1 cu 8, notați restul și coeficientul. Atribuiți valoarea R2 și Q2 restului și cuentului obținute în acest pas.
- Pasul 3: Repetați secvența până când obțineți o valoare a coeficientului (Qn) egală cu 0.
- Pasul 4: Numărul octal va arăta cam așa: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Exemplu: Să considerăm un număr zecimal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Așadar, echivalentul OCTAL al lui 2181 este:
(2181) Decimal = (4205) Octal
Conversia sistemului numeric octal în sistem binar:
Din nou, conversia din octal în zecimal este foarte asemănătoare cu conversia din binar în zecimal, singura diferență este că de data aceasta vom înmulți cifrele cu puterile lui 8 în loc de 2. Conversia se poate face urmând pașii de mai jos:
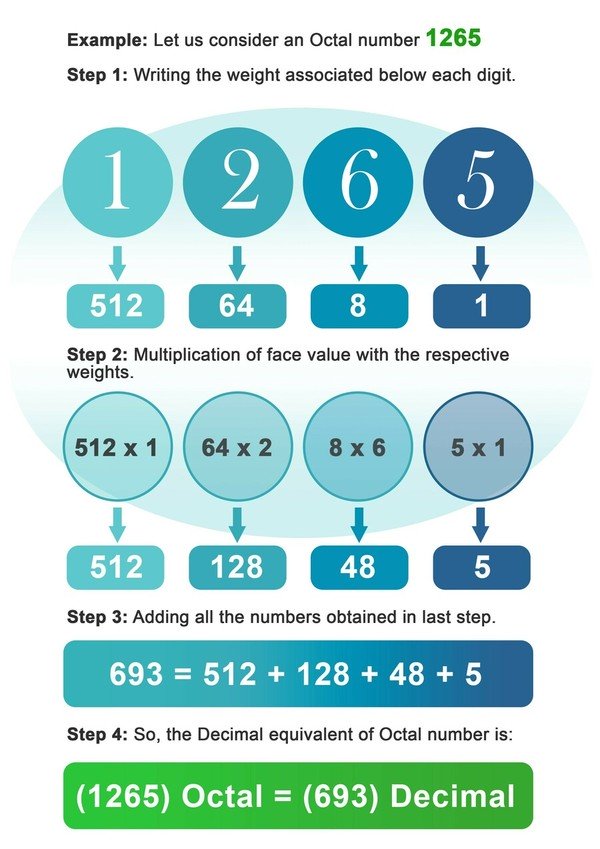
- Pasul 1: Scrieți greutatea lui 8 asociată sub fiecare cifră a numărului octal.
- Pasul 2: Acum se înmulțește fiecare cifră cu greutatea asociată la acel loc sau indice al cifrei.
- Pasul 3: Adunați toate numerele obținute în urma înmulțirii din pasul anterior.
- Pasul 4: Numărul obținut în ultimul pas este echivalentul zecimal al numărului octal.
Exemplu: Să luăm în considerare un număr octal 1265.