Как конвертировать октябрьскую и десятичную системы счисления?
Прежде чем перейти к разговору о преобразовании одной системы номеров в другую, давайте немного поговорим о самой системе номеров. Система чисел может быть определена как набор различных комбинаций символов, каждый из которых имеет свой вес. Любая система счисления дифференцируется по радиксу или основе, на которой строится система счисления. Радикс или база определяет общее отсутствие различных символов, которое используется в определенной системе счисления. Например, радикс двоичной системы счисления равен 2, радикс десятичной системы счисления - 10, а радикс восьмеричной системы счисления - 8.
Октальная система номеров:
Как явствует из названия, эта система счисления основана на радиусе, равном 8. Итак, в этой системе счисления мы имеем восемь различных цифр. Для простоты мы считаем эти восемь цифр такими же, как и первые восемь цифр в десятичной системе счисления. Положение каждой восьмеричной цифры связано с некоторой силой 8, и эта сила равна показателю цифры от левой позиции. Для представления одного восьмеричного числа в двоичной форме требуется не более трех двоичных цифр. Так как основа этой числовой системы сама по себе имеет некоторую силу двойки, то очень легко и удобно перевести восьмеричное число в двоичную или шестнадцатеричную систему счисления, которая используется в компьютерах для выполнения всей работы.
Октальные числа не находят прямого применения в компьютерной технике, потому что компьютеры работают в двоичных состояниях или битах. Однако, поскольку восьмеричное число занимает меньше цифр для представления в двоичном виде, его можно эффективно хранить в памяти компьютера, не тратя впустую места, например, BCD(Binary Coded Decimal) число.
Преобразование десятичной системы счисления в октябрьскую:
Преобразование десятичной дроби в восьмеричную очень похоже на преобразование десятичной дроби в двоичную. Единственная разница заключается в том, что на этот раз мы разделим десятичное число на 8 вместо 2. Преобразование может быть выполнено следующим образом:
- Шаг 1: Разделите десятичное число на 8, запишите остаток и присвойте ему значение R1. Аналогично, запишите коэффициент и присвойте ему значение Q1.
- Шаг 2: Теперь разделите Q1 на 8, отметьте остаток и коэффициент. Присваиваем значение R2 и Q2 остатку и коэффициенту, полученному на этом шаге.
- Шаг 3: Повторяйте последовательность до тех пор, пока не получите значение коэффициента (Qn), равное 0.
- Шаг 4: Восьмеричное число будет выглядеть так.: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Пример: Рассмотрим десятичное число 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Итак, ОКТАЛЬНЫЙ эквивалент 2181:
(2181) Decimal = (4205) Octal
Преобразование октября в двоичную систему счисления:
Опять же, преобразование восьмеричного числа в десятичное очень похоже на преобразование двоичного числа в десятичное, разница лишь в том, что на этот раз мы будем умножать цифры с силой 8, а не 2. Преобразование может быть выполнено с помощью описанных ниже шагов:
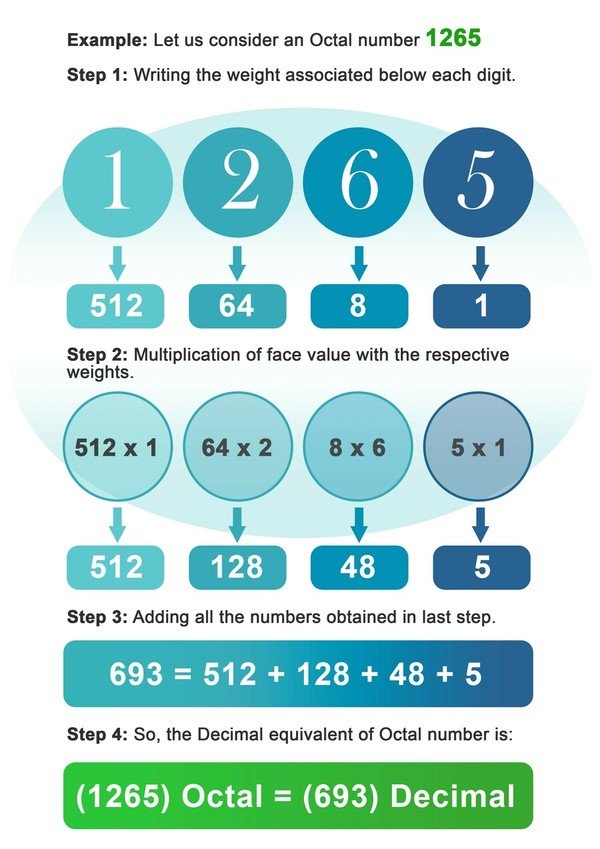
- Шаг 1: Запишите вес 8, связанный с каждой цифрой восьмеричного числа.
- Шаг 2: Теперь умножьте каждую цифру с весом, ассоциируемым с этим местом или индексом цифры.
- Шаг 3: Добавьте все числа, полученные после умножения на предыдущем шаге.
- Шаг 4: Число, полученное на последнем шаге, является десятичным эквивалентом восьмеричного числа.
Пример: Рассмотрим октябрьское число 1265.