Hoe kan men tussen het Oktal- en het Decimale Getalsysteem omrekenen?
Voordat we in het gesprek gaan over het omzetten van het ene nummersysteem in het andere, laten we het eerst even hebben over het Nummersysteem zelf. Nummersysteem kan worden gedefinieerd als de set van de verschillende combinaties van symbolen, waarbij elk symbool een bepaald gewicht heeft. Elk getallensysteem wordt gedifferentieerd op basis van de radix of de basis waarop het getallensysteem is gemaakt. Radix of de basis definieert het totaal aantal verschillende symbolen, dat in een bepaald nummersysteem wordt gebruikt. Bijvoorbeeld, de radix van het Binaire getallenstelsel is 2, de radix van het decimale getallenstelsel is 10, en de radix van het octale getallenstelsel is 8.
Het oktaalnummersysteem:
Zoals de naam duidelijk aangeeft, is dit nummersysteem gebaseerd op een radix gelijk aan 8. In dit nummersysteem hebben we dus acht verschillende cijfers. Voor het gemak beschouwen we deze acht cijfers als hetzelfde als de eerste acht cijfers in het decimale getallenstelsel. De positie van elk octaal cijfer is geassocieerd met een zekere macht van 8 en deze macht is gelijk aan de index van het cijfer uit de linker positie. Er zijn maximaal drie binaire cijfers nodig om een binair octaal getal weer te geven. Aangezien de basis van dit getallensysteem zelf enige kracht van twee is, is het zeer eenvoudig en handig om het octale getal om te zetten in een binair of hexadecimaal getallensysteem dat in computers wordt gebruikt om al het werk te doen.
Oktale nummers vinden geen directe toepassing in de computermachine omdat computers werken op binaire toestanden of bits. Echter, omdat het octale getal minder cijfer in beslag neemt om in binair te worden weergegeven, kunnen ze efficiënt worden opgeslagen in de computer zonder verspilde ruimte in het geheugen, zoals BCD (Binary Coded Decimal) nummer.
Omrekening van Decimale naar Octale Nummersysteem:
De omrekening van decimaal naar octaal lijkt sterk op het omzetten van decimaal naar binair. Het enige verschil is dat we deze keer het decimaal getal delen door 8 in plaats van 2. De omrekening kan gedaan worden door de onderstaande schriftelijke stappen te volgen:
- Stap1: Deel het decimaal getal door 8, noteer de rest en geef er de waarde R1 aan toe. Noteer op dezelfde manier het quotiënt en wijs er de waarde Q1 aan toe.
- Stap 2: Verdeel nu Q1 met 8, let op de rest en het quotiënt. Wijs de waarde R2 en Q2 toe aan de rest en het quotiënt dat in deze stap wordt verkregen.
- Stap 3: Herhaal de reeks totdat u de waarde van het quotiënt (Qn) gelijk aan 0 krijgt.
- Stap4: Het octale getal zal er zo uitzien: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Voorbeeld: Laten we eens kijken naar een decimaal getal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Dus, het OCTAL equivalent van 2181 is:
(2181) Decimal = (4205) Octal
Omrekening van Octal naar Binary Number System:
Nogmaals, de omzetting van octaal in decimaal is zeer vergelijkbaar met de omzetting van binair in decimaal, het enige verschil is dat we deze keer de cijfers zullen vermenigvuldigen met de bevoegdheden van 8 in plaats van 2. De omzetting kan worden gedaan door het volgen van de onderstaande schriftelijke stappen:
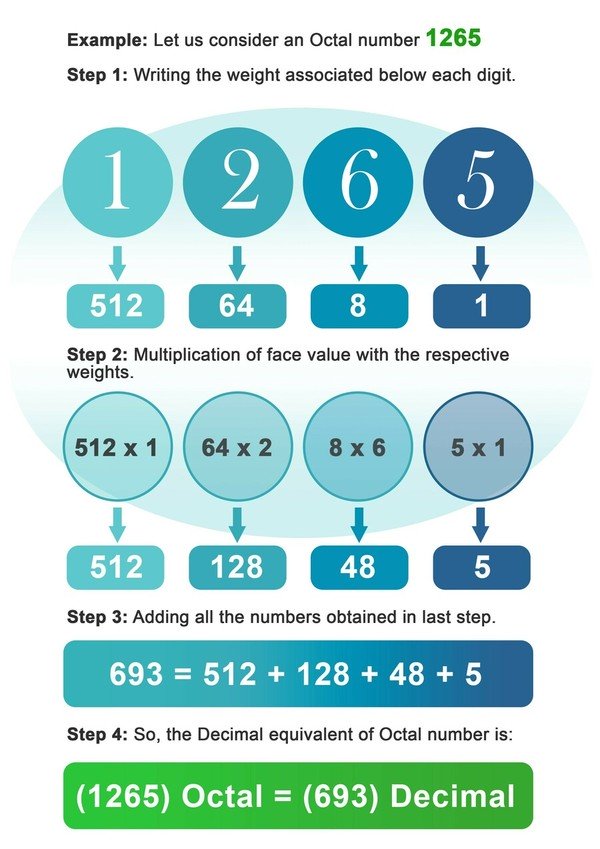
- Stap 1: Noteer het gewicht van 8 onder elk cijfer van het octale getal.
- Stap2: Vermenigvuldig nu elk cijfer met het gewicht dat op die plaats of op die cijferindex hoort.
- Stap 3: Tel alle getallen op die na de vermenigvuldiging in de vorige stap zijn verkregen.
- Stap4: Het getal dat in de laatste stap wordt verkregen is het decimale equivalent van het octale getal.
Voorbeeld: Laten we eens kijken naar een oktal nummer 1265.