Πώς να μετατρέψετε μεταξύ των οκταδικών και δεκαδικών συστημάτων αριθμών;
Πριν ξεκινήσουμε τη συζήτηση για τη μετατροπή ενός αριθμητικού συστήματος σε άλλο, ας μιλήσουμε λίγο για το ίδιο το Αριθμητικό Σύστημα. Το Σύστημα Αριθμών μπορεί να οριστεί ως το σύνολο των διαφορετικών συνδυασμών συμβόλων, με κάθε σύμβολο να έχει ένα συγκεκριμένο βάρος. Οποιοδήποτε Σύστημα Αριθμών διαφοροποιείται με βάση το radix ή τη βάση στην οποία βασίζεται το σύστημα αριθμών. Η ρίζα ή η βάση ορίζει το συνολικό αριθμό των διαφορετικών συμβόλων που χρησιμοποιούνται σε ένα συγκεκριμένο σύστημα αριθμών. Για παράδειγμα, το ρίζωμα του δυαδικού συστήματος αριθμών είναι 2, το ρίζωμα του δεκαδικού συστήματος αριθμών είναι 10 και το ρίζωμα του οκταδικού συστήματος αριθμών είναι 8.
Το οκταδικό σύστημα αριθμών:
Όπως υποδηλώνει σαφώς το όνομά του, αυτό το σύστημα αριθμών βασίζεται σε ρίζα ίση με 8. Έτσι, σε αυτό το αριθμητικό σύστημα έχουμε οκτώ διακριτά ψηφία. Για ευκολία θεωρούμε αυτά τα οκτώ ψηφία ίδια με τα οκτώ πρώτα ψηφία του δεκαδικού συστήματος αριθμών. Η θέση κάθε οκταδικού ψηφίου συνδέεται με κάποια δύναμη του 8 και αυτή η δύναμη ισούται με τον δείκτη του ψηφίου από την αριστερή θέση. Χρειάζονται το πολύ τρία δυαδικά ψηφία για την αναπαράσταση ενός οκταδικού αριθμού σε δυαδική μορφή. Καθώς η βάση αυτού του αριθμητικού συστήματος είναι κάποια δύναμη του δύο, είναι πολύ εύκολο και βολικό να μετατραπούν οι οκταδικοί αριθμοί σε δυαδικό ή δεκαεξαδικό σύστημα αριθμών, τα οποία χρησιμοποιούνται στους υπολογιστές για την εκτέλεση όλων των εργασιών.
Οι οκταδικοί αριθμοί δεν βρίσκουν άμεση εφαρμογή στα μηχανήματα των υπολογιστών, επειδή οι υπολογιστές λειτουργούν με δυαδικές καταστάσεις ή bits. Ωστόσο, καθώς οι οκταδικοί αριθμοί καταλαμβάνουν λιγότερα ψηφία για να αναπαρασταθούν σε δυαδικό σύστημα, μπορούν να αποθηκευτούν αποτελεσματικά στον υπολογιστή χωρίς να σπαταληθεί χώρος στη μνήμη, όπως οι αριθμοί BCD (δυαδικός κωδικοποιημένος δεκαδικός αριθμός).
Μετατροπή του δεκαδικού σε οκταδικό σύστημα αριθμών:
Η μετατροπή του δεκαδικού σε οκταδικό είναι πολύ παρόμοια με τη μετατροπή του δεκαδικού σε δυαδικό. Η μόνη διαφορά είναι ότι αυτή τη φορά θα διαιρέσουμε τον δεκαδικό αριθμό με το 8 αντί για το 2. Η μετατροπή μπορεί να γίνει ακολουθώντας τα παρακάτω βήματα:
- Βήμα1: Διαιρέστε τον δεκαδικό αριθμό με το 8, σημειώστε το υπόλοιπο και δώστε του την τιμή R1. Ομοίως, σημειώστε το πηλίκο και αναθέστε του την τιμή Q1.
- Βήμα2: Τώρα διαιρέστε το Q1 με το 8, σημειώστε το υπόλοιπο και το πηλίκο. Αναθέστε την τιμή R2 και Q2 στο υπόλοιπο και στο πηλίκο που προέκυψαν σε αυτό το βήμα.
- Βήμα3: Επαναλάβετε την ακολουθία μέχρι να λάβετε την τιμή του πηλίκου (Qn) ίση με 0.
- Βήμα4: Ο οκταδικός αριθμός θα μοιάζει κάπως έτσι: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Παράδειγμα: Ας θεωρήσουμε έναν δεκαδικό αριθμό 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Έτσι, το ισοδύναμο OCTAL του 2181 είναι:
(2181) Decimal = (4205) Octal
Μετατροπή του οκταδικού σε δυαδικό σύστημα αριθμών:
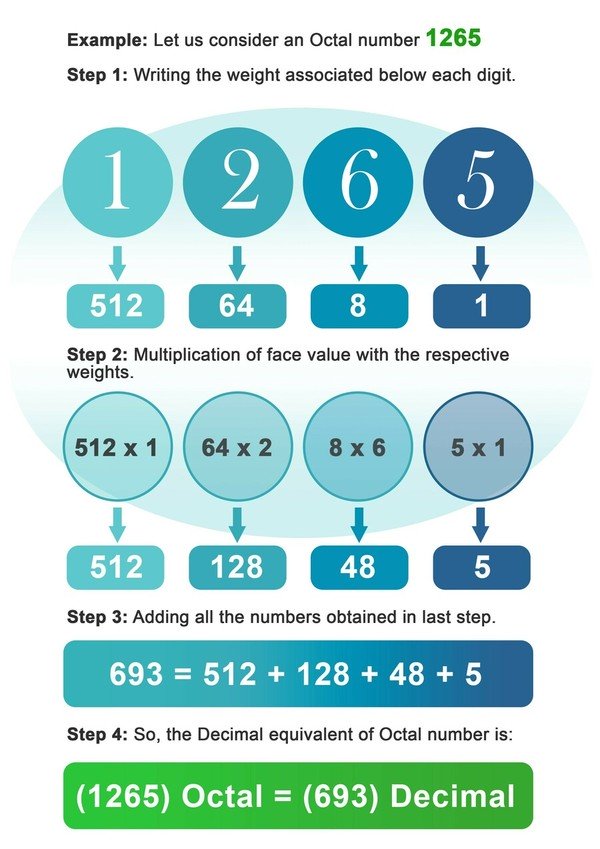
Και πάλι, η μετατροπή του οκταδικού σε δεκαδικό μοιάζει πολύ με τη μετατροπή του δυαδικού σε δεκαδικό, με τη μόνη διαφορά ότι αυτή τη φορά θα πολλαπλασιάσουμε τα ψηφία με τις δυνάμεις του 8 αντί του 2. Η μετατροπή μπορεί να γίνει ακολουθώντας τα παρακάτω βήματα:
- Βήμα 1: Γράψτε το βάρος του 8 που συνδέεται κάτω από κάθε ψηφίο του οκταδικού αριθμού.
- Βήμα2: Τώρα πολλαπλασιάστε κάθε ψηφίο με το βάρος που σχετίζεται με τη συγκεκριμένη θέση ή το δείκτη του ψηφίου.
- Βήμα3: Προσθέστε όλους τους αριθμούς που προέκυψαν μετά τον πολλαπλασιασμό στο προηγούμενο βήμα.
- Βήμα4: Ο αριθμός που λαμβάνεται στο τελευταίο βήμα είναι το δεκαδικό ισοδύναμο του οκταδικού αριθμού.
Παράδειγμα: Ας θεωρήσουμε έναν οκταδικό αριθμό 1265.