Sekizli ve Ondalık Sayı Sistemleri arasında nasıl dönüşüm yapılır?
Bir sayı sisteminin diğerine dönüştürülmesi konusuna girmeden önce, Sayı Sisteminin kendisi hakkında biraz konuşalım. Sayı Sistemi, her bir sembolün belirli bir ağırlığa sahip olduğu farklı sembol kombinasyonlarının kümesi olarak tanımlanabilir. Herhangi bir Sayı Sistemi, radiks veya sayı sisteminin yapıldığı taban temelinde farklılaştırılır. Radiks veya Taban, belirli bir sayı sisteminde kullanılan farklı sembollerin toplam sayısını tanımlar. Örneğin, İkili sayı sisteminin radiksi 2, ondalık sayı sisteminin radiksi 10 ve sekizli sayı sisteminin radiksi 8'dir.
Sekizli Sayı Sistemi:
Adından da anlaşılacağı üzere, bu sayı sistemi 8'e eşit bir radikse dayanmaktadır. Yani, bu sayı sisteminde sekiz farklı rakamımız vardır. Kolaylık olması açısından bu sekiz basamağı ondalık sayı sistemindeki ilk sekiz basamakla aynı kabul ediyoruz. Her sekizli rakamın konumu 8'in bir kuvveti ile ilişkilidir ve bu kuvvet sol konumdan itibaren rakamın indeksine eşittir. Bir sekizli sayıyı ikili biçimde temsil etmek için en fazla üç ikili basamak gerekir. Bu sayı sisteminin tabanı ikinin bir kuvveti olduğundan, sekizli sayıyı bilgisayarlarda tüm işleri yapmak için kullanılan ikili veya onaltılı sayı sistemine dönüştürmek çok kolay ve kullanışlıdır.
Sekizli sayılar bilgisayar makinelerinde doğrudan uygulama alanı bulmaz çünkü bilgisayarlar ikili durumlar veya bitler üzerinde çalışır. Bununla birlikte, sekizli sayılar ikili olarak temsil edilmek için daha az basamak işgal ettiğinden, BCD (İkili Kodlanmış Ondalık) sayı gibi bellekte boşa yer harcamadan bilgisayarda verimli bir şekilde saklanabilirler.
Ondalık Sayı Sisteminin Sekizlik Sayı Sistemine Dönüştürülmesi:
Ondalık sayının sekizlik sayıya dönüştürülmesi, ondalık sayının ikili sayıya dönüştürülmesine çok benzer. Tek fark, bu sefer ondalık sayıyı 2 yerine 8'e böleceğiz. Dönüşüm aşağıda yazılı adımlar izlenerek yapılabilir:
- Adım1: Ondalık sayıyı 8'e bölün, kalanı not edin ve ona R1 değerini atayın. Benzer şekilde, bölümü not edin ve ona Q1 değerini atayın.
- Adım2: Şimdi Q1'i 8'e bölün, kalanı ve bölümü not edin. Bu adımda elde edilen kalana ve bölüme R2 ve Q2 değerlerini atayın.
- Adım3: Bölüm (Qn) değeri 0'a eşit olana kadar diziyi tekrarlayın.
- Adım4: Sekizli sayı aşağıdaki gibi görünecektir: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Örnek: Ondalık bir sayı olan 2181'i ele alalım.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Yani 2181'in OCTAL karşılığı şudur:
(2181) Decimal = (4205) Octal
Sekizli Sayı Sisteminin İkili Sayı Sistemine Dönüştürülmesi:
Yine, sekizli sayının onlu sayıya dönüştürülmesi, ikili sayının onlu sayıya dönüştürülmesine çok benzer, tek fark bu kez basamakları 2 yerine 8'in kuvvetleriyle çarpacağız. Dönüşüm aşağıda yazılı adımlar izlenerek yapılabilir:
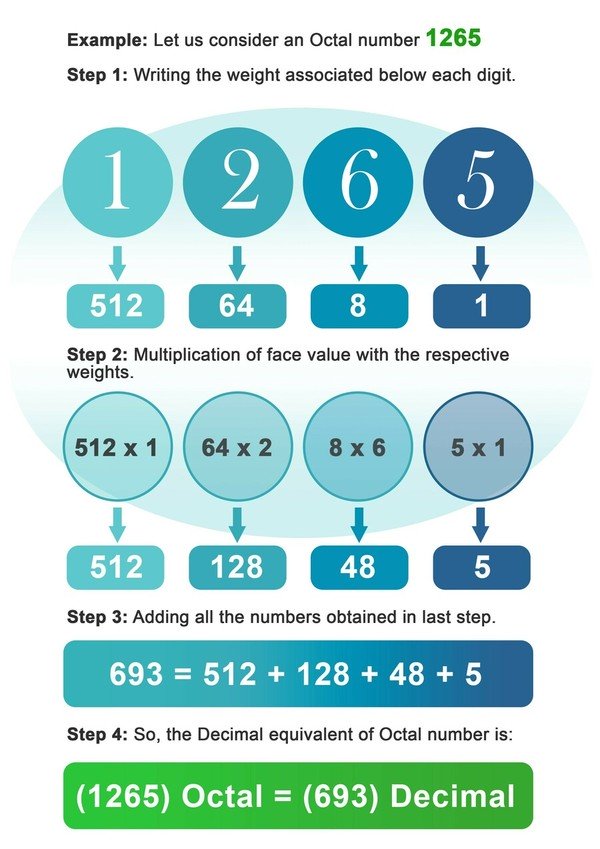
- Adım 1: Sekizli sayının her basamağının altına ilişkili 8'in ağırlığını yazın.
- Adım 2: Şimdi her bir rakamı o yerdeki veya rakam indeksindeki ağırlık ile çarpın.
- Adım3: Bir önceki adımda çarpma işleminden sonra elde edilen tüm sayıları toplayın.
- Adım4: Son adımda elde edilen sayı sekizlik sayının ondalık karşılığıdır.
Örnek: Sekizli bir sayı olan 1265'i ele alalım.