Kako pretvoriti osmiški in desetiški številski sistem?
Preden se lotimo pretvorbe enega številskega sistema v drugega, spregovorimo nekaj besed o samem številskem sistemu. Številski sistem lahko opredelimo kot množico različnih kombinacij simbolov, pri čemer ima vsak simbol določeno težo. Vsak številski sistem se razlikuje glede na radiks ali osnovo, na kateri je številski sistem narejen. Radix ali osnova določa skupno število različnih simbolov, ki se uporabljajo v določenem številskem sistemu. Na primer, radix dvojiškega številskega sistema je 2, radix desetiškega številskega sistema je 10, radix osmeriškega številskega sistema pa 8.
Oktalni številski sistem:
Kot je razvidno iz imena, ta številski sistem temelji na radixu, ki je enak 8. V tem številskem sistemu imamo torej osem različnih števk. Za lažjo predstavo teh osem števk obravnavamo enako kot prvih osem števk v desetiškem številskem sistemu. Položaj vsake osmiške številke je povezan z neko močjo 8, ta moč pa je enaka indeksu številke z levega položaja. Za predstavitev enega osmiškega števila v binarni obliki so potrebne največ tri binarne številke. Ker je osnova tega številskega sistema sama po sebi neka moč dveh, je zelo enostavno in priročno pretvoriti osmiško število v dvojiški ali šestnajstiški številski sistem, ki se uporablja v računalnikih za opravljanje vsega dela.
Oktalna števila se ne uporabljajo neposredno v računalniški tehniki, saj računalniki delujejo na podlagi binarnih stanj ali bitov. Ker pa osmerokotna števila zavzemajo manj številk za predstavitev v binarni obliki, jih je mogoče učinkovito shraniti v računalnik brez izgube prostora v pomnilniku, tako kot števila BCD (binarno kodirana decimalna števila).
Pretvorba desetiškega v osmiški številski sistem:
Pretvorba decimalnega v oktalno število je zelo podobna pretvorbi decimalnega v binarno število. Edina razlika je, da bomo tokrat decimalno število namesto z 2 delili z 8. Pretvorbo lahko izvedemo po spodaj zapisanih korakih:
- 1. korak: decimalno število delimo z 8, zapišemo ostanek in mu pripišemo vrednost R1. Podobno zapišite količnik in mu pripišite vrednost Q1.
- Korak2: Sedaj delite Q1 z 8, zapišite ostanek in kvocient. Vrednost R2 in Q2 pripišite preostanku in kvocientu, ki ju dobite v tem koraku.
- Korak3: Zaporedje ponavljajte, dokler ne dobite vrednosti količnika (Qn), ki je enaka 0.
- Korak4: Osmiško število bo videti nekako takole: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Primer: Vzemimo decimalno število 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Tako je ekvivalent 2181 v sistemu OCTAL naslednji:
(2181) Decimal = (4205) Octal
Pretvorba oktalnega v binarni številski sistem:
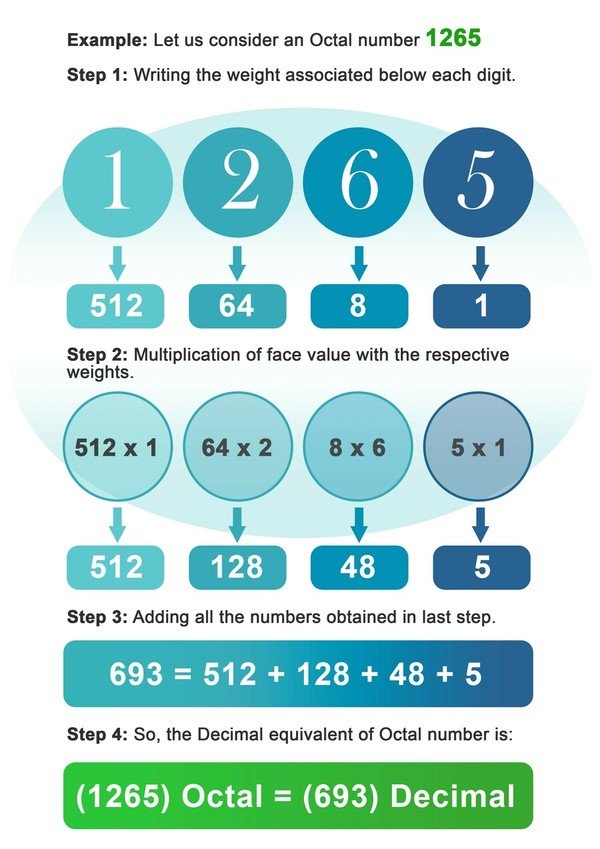
Pretvorba osmiške v desetiško število je spet zelo podobna pretvorbi dvojiške v desetiško število, s to razliko, da bomo tokrat števke pomnožili z močjo 8 namesto z 2. Pretvorbo lahko izvedemo po spodaj zapisanih korakih:
- Korak 1: Pod vsako številko osmerokotnega števila zapišite težo 8, ki je povezana z njim.
- Korak2: Zdaj pomnožite vsako številko z utežjo, povezano s tem mestom ali indeksom številke.
- Korak3: Seštejte vsa števila, ki ste jih dobili po množenju v prejšnjem koraku.
- Korak4: Število, dobljeno v zadnjem koraku, je decimalni ekvivalent osmiškega števila.
Primer: Vzemimo oktalno število 1265.