Hvordan konvertere mellom det oktale og desimalt tallsystemet?
Før vi går inn på samtalen om konvertering av et tallsystem til et annet, skal vi snakke litt om tallsystemet selv. Tallsystemet kan defineres som settet med forskjellige kombinasjoner av symboler, der hvert symbol har en bestemt vekt. Ethvert tallsystem differensieres på grunnlag av radiksen eller basen som tallsystemet er laget for. Radiksen eller basen definerer det totale antallet forskjellige symboler som brukes i et bestemt tallsystem. For eksempel er radiksen i det binære tallsystemet 2, radiksen i det desimale tallsystemet er 10, og radiksen i det oktale tallsystemet er 8.
Oktalsystemet:
Som navnet tydelig indikerer, er dette tallsystemet basert på grunntallet 8. Så i dette tallsystemet har vi åtte ulike siffer. For enkelhets skyld betrakter vi disse åtte sifrene som de samme som de første åtte sifrene i det desimale tallsystemet. Plasseringen av hvert oktalsiffer er knyttet til en potens av 8, og denne potensen er lik indeksen til sifferet fra venstre. Det tar maksimalt tre binære sifre å representere ett oktaltall i binær form. Siden grunntallet i dette tallsystemet er en potens av to, er det veldig enkelt og praktisk å konvertere oktaltall til binært eller heksadesimalt tallsystem, som brukes i datamaskiner for å gjøre alt arbeidet.
Oktagonale tall har ikke direkte anvendelse i datamaskiner fordi datamaskiner arbeider med binære tilstander eller biter. Imidlertid oktale nummer okkupere mindre siffer for å bli representert i binær så de kan lagres effektivt i datamaskinen uten noe bortkastet plass i minnet som BCD (binært kodet desimal) nummer.
Konvertering av desimalt til oktalt tallsystem:
Konvertering av desimalt til oktaltall er svært lik konvertering av desimalt til binært. Den eneste forskjellen er at vi denne gangen skal dele det desimale tallet med 8 i stedet for 2. Konverteringen kan gjøres ved å følge de nedenfor skrevne trinnene:
- Trinn 1: Del det desimale tallet med 8, noter resten og tildel den verdien R1. På samme måte, noter kvotienten og tildel den verdien Q1.
- Trinn 2: Del nå Q1 med 8, noter resten og kvotienten. Tildel verdien R2 og Q2 til resten og kvotienten som er oppnådd i dette trinnet.
- Trinn 3: Gjenta sekvensen til du får verdien av kvotienten (Qn) lik 0.
- Trinn 4: Oktaltalet vil sjå noko slikt ut : Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Eksempel: La oss ta et desimalt tall 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Oktaltallet som tilsvarer 2181, er:
(2181) Decimal = (4205) Octal
Konvertering av oktale til binært tallsystem:
Igjen, konvertering av oktal til desimal er veldig lik konvertering av binær til desimal, den eneste forskjellen er at vi denne gangen vil multiplisere sifrene med potensene av 8 i stedet for 2. Konverteringen kan gjøres ved å følge de nedenfor skrevne trinnene:
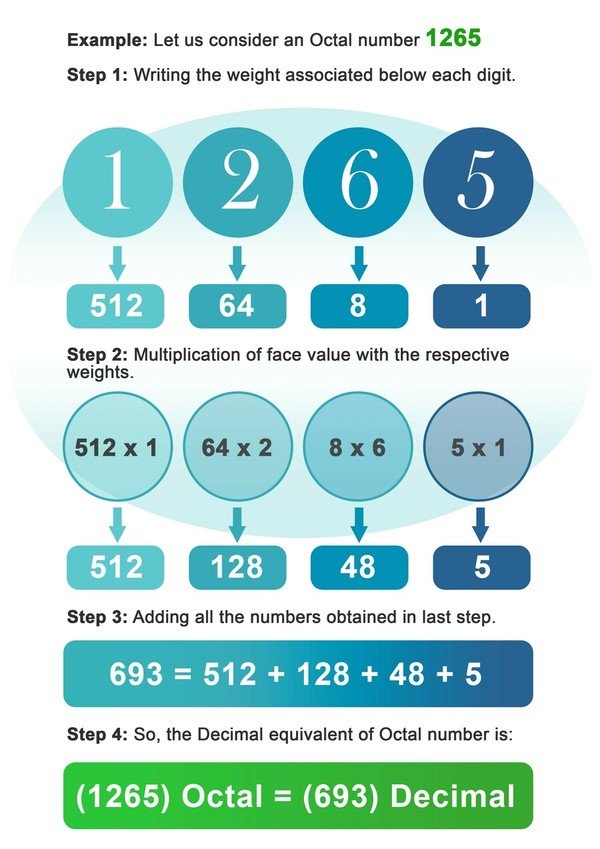
- Trinn 1: Skriv ned vekten av 8 assosierte nedenfor hvert siffer i det oktale tallet.
- Trinn 2: Multipliser nå hvert siffer med vekten som er knyttet til den plassen eller indeksen til sifferet.
- Trinn3: Legg sammen alle tallene som er oppnådd etter multiplikasjon i forrige trinn.
- Trinn 4: Tallet som ble funnet i forrige trinn, er den desimale ekvivalenten til det oktale tallet.
Eksempel: La oss se på et oktalt tall 1265.