如何在八進制和十進制數字系統之間轉換?
在談論將一個數字系統轉換為另一個之前,讓我們稍微談一下數字系統本身。數字系統可以被定義為一組不同符號的組合,每個符號都有特定的權重。任何數字系統都是根據基數或基數來區分的,基數或基數定義了在特定數字系統中使用的不同符號的總數。例如,二進制數字系統的基數是2,十進制數字系統的基數是10,八進制數字系統的基數是8。
八進位制:
如名字清楚表示,此數字系統基於基數為8。因此,在此數字系統中,我們有八個不同的數字。為了方便起見,我們將這八個數字視為與十進制數字系統中的前八個數字相同。每個八進制數位的位置與8的某個次方相關聯,並且該次方等於該數位從左側位置計算的索引。在二進制形式中,表示一個八進制數最多需要三位二進制數字。由於此數字系統的基數本身是二的某個次方,所以將八進制數轉換為二進制或十六進制數字系統非常容易和方便,而這些數字系統在計算機中用於執行所有工作。
八進制數字在計算機機器上並沒有直接應用,因為計算機是以二進制狀態或位元來運作的。然而,由於八進制數字佔用的位數較少,可以有效地在計算機中儲存,而不會像二進制編碼十進制(BCD)數字一樣浪費記憶體空間。
十进制数转换为八进制数系统:
小數轉為八進位是非常類似於將十進位轉為二進位的方式。唯一的不同是,這次我們要將十進位數字除以8而不是2。可以按照下面的步驟進行轉換:
- 步驟1:將十進制數字除以8,記下餘數並將其指定為R1的值。同樣地,記下商並將其指定為Q1的值。
- Step2:現在將 Q1 除以8,注意餘數和商數。將在此步驟中獲得的餘數和商數分別賦值為 R2 和 Q2。
- 第三步:重複該序列直到商(Qn)的值等於0。
- Step4: 八進位數字看起來會像這樣: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
讓我們考慮一個十進制數字2181。
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
所以,2181的八進制等價為:4065
(2181) Decimal = (4205) Octal
Conversion of Octal into Binary Number System: 將八進位數轉換為二進位數系統:
再者,從八進制轉換為十進制與從二進制轉換為十進制非常相似,唯一的區別是這次我們將數字乘以8的冪次而不是2。可以通過以下步驟進行轉換:
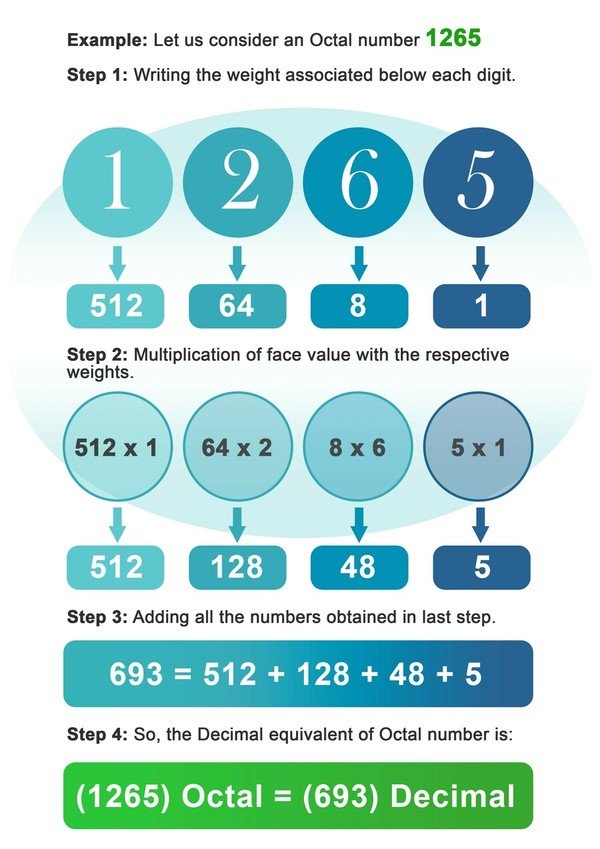
- 步驟1:在八進制數字的每個位數下方寫下相應的重量。
- 第二步:現在將每個數字與其所在位數或索引的權重相乘。
- 步驟3:將前一步驟中獲得的數字相乘後,將所有數字相加。
- 第4步:上一步得到的數字是八進位數的十進位等值。
請我們考慮一個八進制數字1265。