ตัวแปลงแปลงเลขฐานแปดเป็นเลขฐานสิบ

วิธีแปลงจากระบบตัวเลขแปดเป็นฐานสิบย่อย

ก่อนที่จะเข้าสู่การสนทนาเกี่ยวกับการแปลงระบบหมายเลขหนึ่งเป็นระบบอื่น ให้เรามาพูดคุยเล็กน้อยเกี่ยวกับระบบหมายเลขเอง ระบบหมายเลขสามารถนิยามได้เป็นเซ็ตของการรวมตัวกันที่แตกต่างกันของสัญลักษณ์ โดยแต่ละสัญลักษณ์มีน้ำหนักที่แตกต่างกัน ระบบหมายเลขใดๆ จะแตกต่างกันขึ้นอยู่กับฐานหรือฐานที่ระบบหมายเลขถูกสร้างบน ฐานหรือฐานกำหนดจำนวนสัญลักษณ์ทั้งหมดที่ใช้ในระบบหมายเลขนั้นๆ ตัวอย่างเช่น ฐานของระบบเลขฐานสองคือ 2 ฐานของระบบเลขสิบคือ 10 และฐานของระบบเลขแปดคือ 8

ระบบตัวเลขแปดเลข:

ตามที่ชื่อแสดงอย่างชัดเจน ระบบจำนวนนี้จะขึ้นอยู่กับฐานที่เท่ากับ 8 ดังนั้น ในระบบจำนวนนี้เรามีตัวเลขแปดตัวที่แตกต่างกัน สำหรับความง่ายเราจะพิจารณาตัวเลขแปดตัวนี้เหมือนกับตัวเลขแปดตัวแรกในระบบตัวเลขทศนิยม ตำแหน่งของแต่ละหลักแปดเกี่ยวข้องกับกำลังของ 8 และกำลังนี้เท่ากับดัชนีของตัวเลขจากตำแหน่งซ้าย มันใช้เลขฐานสามถึงสามหลักในการแทนฐานแปดหนึ่งตัวในรูปแบบทศนิยม โดยเนื่องจากฐานของระบบจำนวนนี้เองเป็นกำลังสองบางคู่ดังนั้น มันจึงง่ายและสะดวกที่จะแปลงจำนวนแปดเลขเป็นระบบจำนวนฐานสองหรือสิบหกที่ใช้ในคอมพิวเตอร์เพื่อทำงานทั้งหมด

ตัวเลขแปดฐานไม่มีสถานไหนที่นำไปใช้โดยตรงในเครื่องมือคอมพิวเตอร์เนื่องจากคอมพิวเตอร์ทำงานบนสถานะทยอยฐานสองหรือบิต อย่างไรนัก เนื่องจากตัวเลขแปดฐานเบสแปดน้อยกว่าหลักเพื่อแสดงในรูปแบบไบนารี เราจึงสามารถบันทึกตัวเลขลงในคอมพิวเตอร์ได้อย่างมีประสิทธิภาพโดยไม่มีพื้นที่ที่สูญเสียในหน่วยความจำเช่นเลข BCD (Binary Coded Decimal)

แปลงทศนิยมเป็นระบบตัวเลขแปด:

การแปลงทศนิยมเป็นฐานแปดคล้ายกับการแปลงทศนิยมเป็นฐานสอง ความแตกต่างเพียงแต่ครั้งนี้เราจะหารจำนวนทศนิยมด้วย 8 แทน 2 การแปลงสามารถทำได้โดยการปฏิบัติตามขั้นตอนที่เขียนไว้ด้านล่าง:

• Step1: นำจำนวนทศนิยมที่แล้วมาหารด้วย 8 หารลงตัว จดเลขเศษทแยง และกำหนดค่า R1 ให้เป็นเลขเศษ ในทางเดียวกัน จดเลขผลหารและกำหนดค่า Q1 ให้เป็นเลขผลหาร
• ขั้นตอนที่ 2: ทำการหาร Q1 ด้วย 8 แล้วจดเศษที่ได้และเศษที่ได้ กำหนดค่า R2 และ Q2 ให้เป็นเศษที่ได้และค่าที่ได้ในขั้นตอนนี้
• Step3: ทำซ้ำลำดับจนกว่าค่าส่วนหาร (Qn) จะเท่ากับ 0
• ขั้นตอนที่ 4: จำนวนแบบแปดจะมีลักษณะประมาณนี้ : Rn R(n-1) R(n-2) ……………………... R3 R2 R1

ตัวอย่าง: ให้เราพิจารณาจำนวนที่เป็นสิบเลข 2181

1. 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
2. 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
3. 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
4. 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0

ดังนั้น เลขฐาน OCTAL ของ 2181 คือ:

(2181) Decimal = (4205) Octal

การแปลงฐานแปดเป็นระบบเลขฐานสอง:

อีกครั้ง, การแปลงฐานแปดเป็นฐานสิบเลขฐานทั้งหมดคล้ายคลึงกับการแปลงฐานสองเป็นฐานสิบ, ความแตกต่างเพียงแค่ครั้งนี้เราจะคูณตัวเลขด้วยพหุนามของ 8 แทน 2 การแปลงสามารถทำได้โดยการปฏิบัติตามขั้นตอนดังต่อไปนี้:

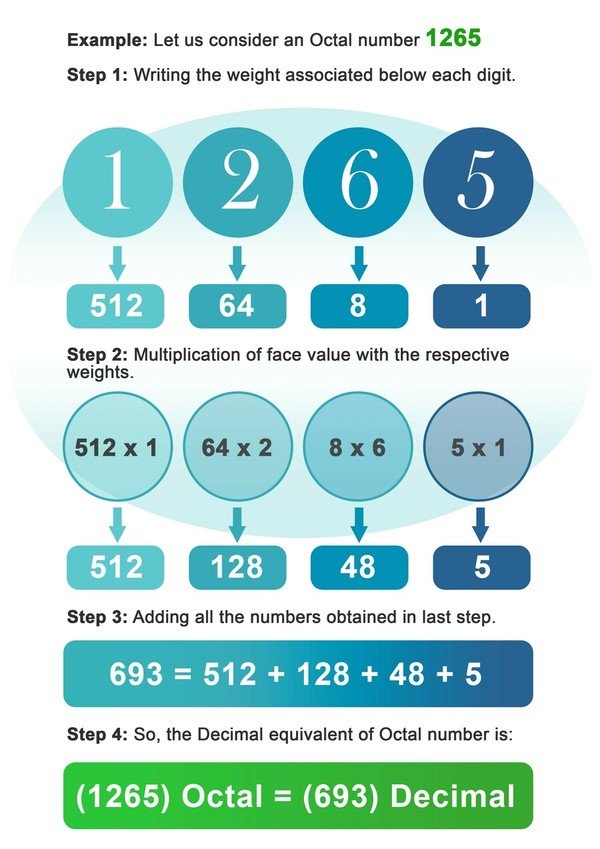
• ขั้นตอนที่ 1: เขียนน้ำหนักรวมของ 8 รอบ ๆ ลงใต้ทุกหลักของตัวเลขแปด
• จากนั้นคูณทุกหลักของตัวเลขด้วยน้ำหนักที่เกี่ยวข้องที่สุดท้ายของดิจิทัลนั้น
• ขั้นตอนที่ 3: บวกเลขทั้งหมดที่ได้หลังจากการคูณในขั้นตอนก่อนหน้า
• ขั้นตอนที่ 4: จำนวนที่ได้จากขั้นตอนล่าสุดคือค่าทศนิยมเทียบเท่าของเลขฐานแปด

ตัวอย่าง: เราจะพิจารณาเลขแปด 1265