如何在八进制和十进制数字系统之间转换?
在讨论将一个数字系统转换为另一个数字系统之前,让我们先谈谈数字系统本身。数字系统可以被定义为不同符号组合的集合,每个符号都有特定的权重。任何数制都是根据数制所依据的基数来区分的。弧度或基数定义了不同符号的总数,这在一个特定的数字系统中使用。例如,二进制数字系统的基数是2,十进制数字系统的基数是10,八进制数字系统的基数是8。
八进制数字系统。
正如其名称所明确表示的那样,这个数字系统是基于等于8的弧度。因此,在这个数字系统中,我们有八个不同的数字。为了方便起见,我们认为这八个数字与十进制数字系统中的前八个数字相同。每个八进制数字的位置都与8的某个幂有关,这个幂等于从左边位置开始的数字的索引。以二进制形式表示一个八进制数最多需要三个二进制数字。由于这个数字系统的基数本身就是2的某个次幂,因此,将八进制数字转换为二进制或十六进制数字系统是非常容易和方便的,这在计算机中被用来做所有的工作。
八进制数在计算机设备中没有直接的应用,因为计算机是在二进制状态或比特上工作。然而,由于八进制数在二进制中占用的数字较少,所以它们可以有效地存储在计算机中,而不会像BCD(二进制编码的十进制)数那样在内存中浪费任何空间。
十进制到八进制数字系统的转换。
十进制到八进制的转换与十进制到二进制的转换非常相似。唯一不同的是,这次我们将用8除以十进制数字,而不是2。
- 第1步:用小数除以8,记下余数并给它赋值R1。同样地,注意商,并给它分配值Q1。
- 第二步:现在用Q1除以8,记下余数和商。将R2和Q2的值分配给本步骤中得到的余数和商。
- 第三步:重复这个序列,直到你得到商的值(Qn)等于0。
- 第四步:八进制数字将看起来像这样: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
例子。 让我们考虑一个十进制数字2181。
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
因此,2181的OCTAL等价物是。
(2181) Decimal = (4205) Octal
八进制转换为二进制数字系统。
同样,八进制转换为十进制与二进制转换为十进制非常相似,唯一不同的是,这次我们将把数字乘以8的幂而不是2。
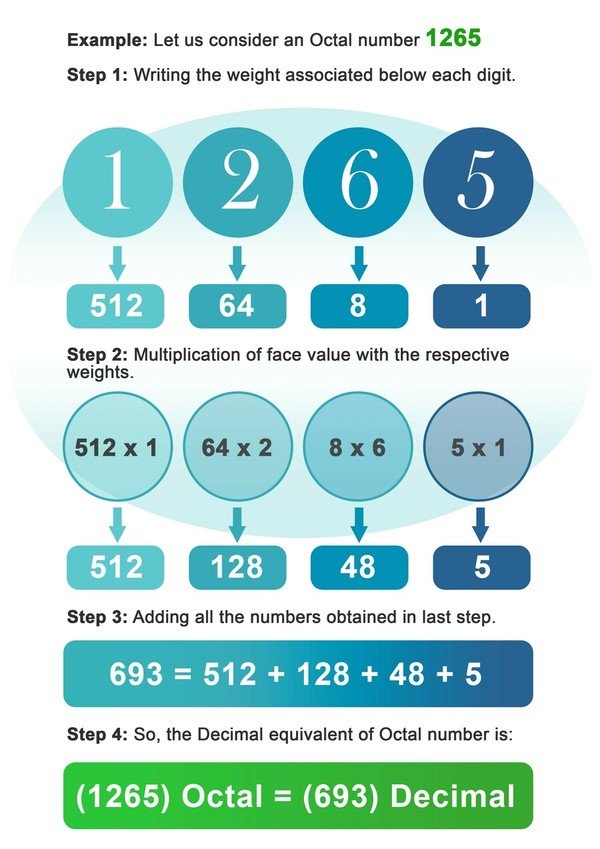
- 第1步:在八进制数字的每个数字下面写下8的重量。
- 第二步:现在将每个数字与该位置或数字索引的相关权重相乘。
- 第三步:将上一步乘法后得到的所有数字相加。
- 第四步:最后一步得到的数字是八进制数字的十进制等值。
例子。让我们考虑一个八进制数字1265。