Kaip konvertuoti dešimtainę ir dešimtainę skaičių sistemas?
Prieš pradėdami pokalbį apie vienos skaičių sistemos keitimą į kitą, šiek tiek pakalbėkime apie pačią skaičių sistemą. Skaičių sistemą galima apibrėžti kaip įvairių simbolių kombinacijų rinkinį, kuriame kiekvienas simbolis turi tam tikrą svorį. Bet kuri skaičių sistema skirstoma pagal radiksą arba pagrindą, pagal kurį sudaryta skaičių sistema. Radiksas arba bazė apibrėžia bendrą skirtingų simbolių, naudojamų tam tikroje skaičių sistemoje, skaičių skaičių skaičių sistemą. Pavyzdžiui, dvejetainės skaičių sistemos radiksas yra 2, dešimtainės skaičių sistemos radiksas yra 10, o aštuntainės skaičių sistemos radiksas yra 8.
Aštuonetainė skaičių sistema:
Kaip aiškiai rodo pavadinimas, ši skaičių sistema yra pagrįsta radiksas lygus 8. Taigi šioje skaičių sistemoje yra aštuoni skirtingi skaitmenys. Kad būtų paprasčiau, šiuos aštuonis skaitmenis laikysime tokiais pačiais kaip pirmieji aštuoni dešimtainės skaičių sistemos skaitmenys. Kiekvieno aštuntainio skaitmens padėtis yra susijusi su tam tikra 8 galybe, o ši galybė lygi skaitmens indeksui iš kairės. Vienam aštuntainiam skaičiui dvejetaine forma išreikšti reikia ne daugiau kaip trijų dvejetainių skaitmenų. Kadangi šios skaičių sistemos pagrindas yra tam tikra dviejų galybė, labai lengva ir patogu aštuonetainį skaičių konvertuoti į dvejetainę arba šešioliktainę skaičių sistemą, kuri naudojama kompiuteriuose visiems darbams atlikti.
Aštuonetainiai skaičiai nėra tiesiogiai pritaikomi kompiuterių technikoje, nes kompiuteriai veikia dvejetainių būsenų arba bitų pagrindu. Tačiau aštuonženkliai skaičiai užima mažiau skaitmenų, kuriuos reikia pavaizduoti dvejetainėje sistemoje, todėl juos galima efektyviai saugoti kompiuteryje, nepanaudojant vietos atmintyje, kaip BCD (dvejetainiai koduotas dešimtainis skaičius).
Dešimtainio skaičiaus sistemos konvertavimas į dešimtainę skaičių sistemą:
Dešimtainės sistemos konvertavimas į aštuntainę yra labai panašus į dešimtainės sistemos konvertavimą į dvejetainę. Vienintelis skirtumas tas, kad šį kartą dešimtainį skaičių dalinsime ne iš 2, o iš 8. Konversiją galima atlikti atlikus toliau nurodytus veiksmus:
- 1 veiksmas: dešimtainį skaičių padalykite iš 8, užrašykite likutį ir priskirkite jam reikšmę R1. Panašiai užrašykite kvotą ir priskirkite jai reikšmę Q1.
- 2 veiksmas: dabar padalykite Q1 iš 8, pasižymėkite likutį ir koeficientą. Šiame žingsnyje gautoms liekanai ir kvantimui priskirkite R2 ir Q2 reikšmes.
- 3 veiksmas: kartokite seką, kol gausite koeficientą (Qn), lygų 0.
- 4 veiksmas: Aštuonetainis skaičius atrodys maždaug taip: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Pavyzdys: Panagrinėkime dešimtainį skaičių 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Taigi, 2181 OCTAL atitikmuo yra:
(2181) Decimal = (4205) Octal
Aštuonetainės sistemos konvertavimas į dvejetainę skaičių sistemą:
Vėlgi, aštuonženklio skaičiaus konvertavimas į dešimtainį yra labai panašus į dvejetainio skaičiaus konvertavimą į dešimtainį, skirtumas tik tas, kad šį kartą skaitmenis dauginsime ne iš 2, o iš 8 galybių:
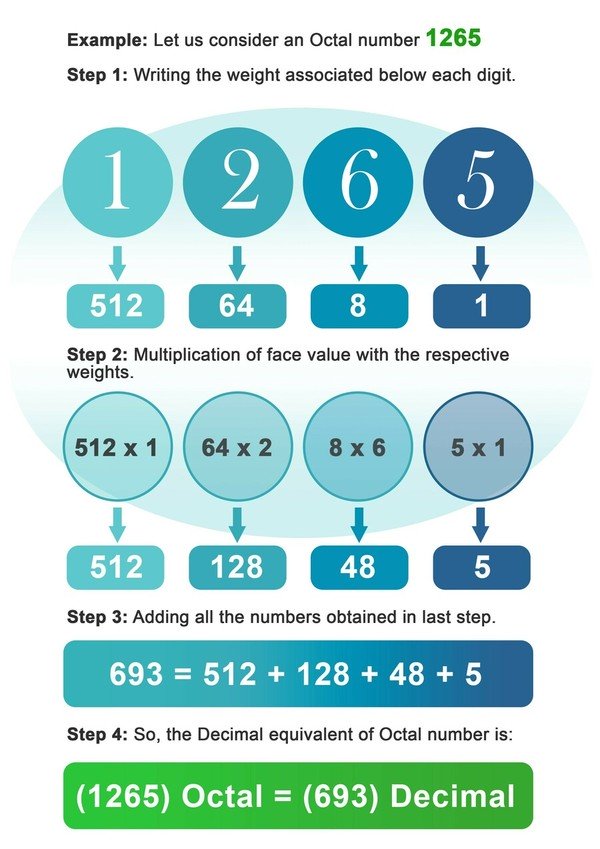
- 1 žingsnis: po kiekvienu aštuntainio skaičiaus skaitmeniu įrašykite 8 svorį.
- 2 veiksmas: dabar kiekvieną skaitmenį padauginkite iš svorio, susijusio su ta vieta arba skaitmenio indeksu.
- 3 veiksmas: Sudėkite visus skaičius, gautus padauginus ankstesniame žingsnyje.
- 4 veiksmas: Paskutiniame veiksme gautas skaičius yra dešimtainis aštuntainio skaičiaus ekvivalentas.
Pavyzdys: Panagrinėkime aštuonetainį skaičių 1265.