Kuidas teisendada oktaal- ja kümnendarvude süsteemi?
Enne, kui hakkame rääkima ühe numbrisüsteemi teisendamisest teise, räägime veidi numbrisüsteemist endast. Numbrisüsteemi võib määratleda kui sümbolite erinevate kombinatsioonide kogumit, kusjuures igal sümbolil on kindel kaal. Iga Numbrisüsteemi eristatakse radiksi ehk baasi alusel, mille alusel see numbrisüsteem on koostatud. Radix või baas määrab erinevate sümbolite koguarvu, mida konkreetses arvusüsteemis kasutatakse. Näiteks binaarse arvusüsteemi radix on 2, kümnendsüsteemi radix on 10 ja kaheksakohalise arvusüsteemi radix on 8.
Oktaalarvude süsteem:
Nagu nimi selgelt näitab, põhineb see arvusüsteem radixil, mis on võrdne 8-ga. Seega on selles numbrisüsteemis kaheksa erinevat numbrit. Lihtsuse huvides peame neid kaheksat numbrit samaks kui kümnendsüsteemi esimesi kaheksat numbrit. Iga kaheksakohalise numbri positsioon on seotud mingi 8-ga ja see võimsus on võrdne numbri indeksiga vasakpoolsest positsioonist. Ühe kaheksakohalise arvu esitamiseks binaarses vormis on vaja maksimaalselt kolm binaarkohta. Kuna selle arvusüsteemi alus on mingi kahevõitu, siis on väga lihtne ja mugav teisendada kaheksakohaline arv binaarseks või heksadekomaalseks arvusüsteemiks, mida kasutatakse arvutites kogu töö tegemiseks.
Oktaalarvud ei leia otsest rakendust arvutimasinates, sest arvutid töötavad binaarsete olekute või bittidega. Kuna aga kaheksakohaline arv võtab vähem numbreid, mida saab esitada binaarselt, siis saab neid tõhusalt salvestada arvutis, ilma et mälus oleks raisatud ruumi, nagu BCD (Binary Coded Decimal) numbrit.
Kümnendsüsteemi konverteerimine kaheksakohaliseks arvusüsteemiks:
Detsimaali teisendamine kaheksakohaliseks on väga sarnane kümnendsüsteemi teisendamisega binaarsüsteemiks. Ainus erinevus on see, et seekord jagame kümnendarvu 2 asemel 8-ga. Ümberarvestust saab teha, järgides allpool kirjeldatud samme:
- 1. samm: Jagage kümnendarv 8-ga, märkige jääk ja määrake sellele väärtus R1. Samamoodi märkige kvooti ja omistage sellele väärtus Q1.
- 2. samm: Nüüd jagage Q1 arvuga 8, märkige jääk ja korrutis. Määrake selles etapis saadud jäägile ja korrutisele väärtus R2 ja Q2.
- 3. samm: Korrake jada, kuni saate kvootiendi (Qn) väärtuseks 0.
- Samm4: Oktaalarv näeb välja umbes nii: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Näide: Vaatleme kümnendarvu 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Seega on 2181 OCTALi ekvivalent 2181:
(2181) Decimal = (4205) Octal
Oktaalarvude konverteerimine binaarsesse arvusüsteemi:
Jällegi on kaheksakohalise teisendamine kümnendsüsteemiks väga sarnane binaarsüsteemi teisendamisega kümnendsüsteemiks, ainus erinevus on see, et seekord korrutame numbreid 2 asemel 8-ga. Teisendamine saab toimuda allpool kirjeldatud samme järgides:
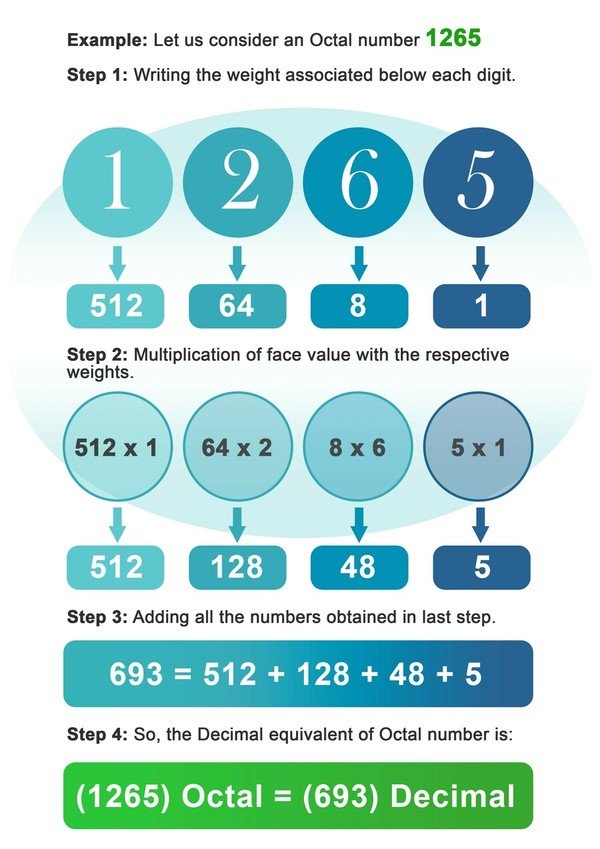
- 1. samm: kirjutage iga kaheksakohalise numbri all oleva 8-ga seotud kaal.
- 2. samm: Nüüd korrutatakse iga number selle koha või numbri indeksiga seotud kaaluga.
- 3. samm: Lisage kõik eelmises etapis saadud arvud kokku pärast korrutamist.
- Samm4: Viimases sammus saadud arv on kaheksakohalise arvu kümnendväärtus.
Näide: Vaatleme oktaalarvu 1265.